题解-CF1396C Monster Invaders

题面

CF1396C Monster Invaders

有 \(n\) 层关卡，每层有 \(a_i\) 个小怪（\(1\) 血）和 \(1\) 个老怪（\(2\) 血）。有三种武器：\(1\) 武器每次攻击耗时 \(r_1\)，可以攻击一个怪 \(1\) 血；\(2\) 武器每次攻击耗时 \(r_2\)，可以攻击一层每个怪 \(1\) 血；\(3\) 武器每次攻击耗时 \(r_3\)，可以杀死一个怪。当一次攻击伤害了老怪但是没有杀死他时，玩家会被迫移动至相邻的层；也可以主动移至相邻的层。刚开始时在 \(1\) 层，每次移动耗时 \(d\)，求最后杀死所有怪的最少耗时（不一定要在 \(n\) 层结束）。

数据范围：\(2\le n\le 10^6\)，\(1\le r_1\le r_2\le r_3\le 10^9\)，\(1\le d\le 10^9\)，\(1\le a_i\le 10^6\)。

---

蒟蒻语

开学前最后一场比赛因为这题卡住了掉回了 CM，真是悲伤。当时少看了 \(r_1\le r_2\le r_3\) 这个条件，AC 后才看到（所以即使没有这个条件蒟蒻的代码可能也可以 AC）。于是彻底失败的蒟蒻决定卧薪尝胆，做了这题写题解。

---

蒟蒻解

首先很明显，打每一层都有两种打法：

• 分次打，先用 \(2\) 或 \(1\) 把 boss 打残，把小兵都打死，然后到时候回来补一刀（用 \(1\)）。

\[st_i=\min(r_2,r_1(a_i+1))+r_1
\]

• 一次打掉，用 \(1\) 把 \(a_i\) 个依次打掉，然后用 \(3\) 把 boss 干掉。

\[pa_i=r_1a_i+r_3
\]

除了 \(st_i\) 和 \(pa_i\)，剩下可以对答案产生贡献的就是如何走位（\(d\) 的贡献）。

假设每个每层如何打已经决定好，且下文中的分界点一定，可以证明如下走位最优：

对于某个分界点后一段选 \(st\) 的，可以到达终点后回来打完（详见样例 \(\#1\) 解释）。

对于分界点前一段的，从 \(1\) 出发：

对于每两个相邻的选 \(st\) 的层对 \(a,b\)，走 \(a\to b\to a\to b\) 的途中将两层打完；

对于多余的选 \(st\) 的层 \(i\)，走 \(i\to i\pm 1\to i\)。

对于选 \(pa\) 的，直接走过就可以。

放个抽象一点的图：

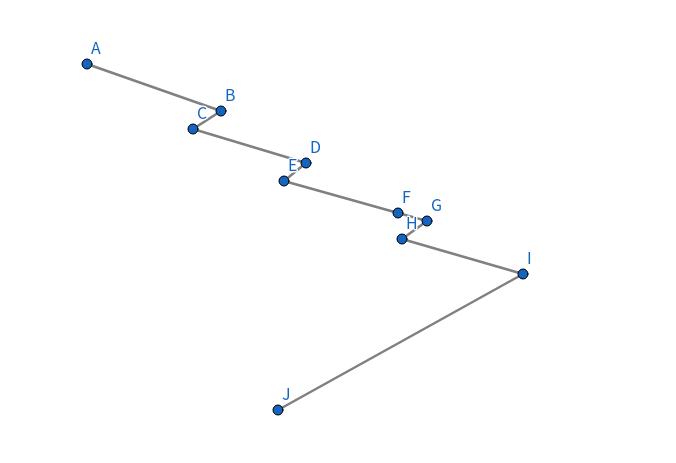
比如样例 \(\#2\)：

打法选择：\([pa,pa,st,st]=6+6+6+8\)。

走位选择：\(1\to 2\to 1\to 2\to 3\to 4=5\)。

所以答案是 \(6+6+6+8+5=31\)。

所以可以先 dp 出以第 \(n\) 层为终点的前 \(i\) 层的最少打法 \(+\) 走位耗时，然后枚举分界点，两边答案加起来取最小值。

---

代码

#include <bits/stdc++.h>
using namespace std;

//Start
typedef long long ll;
typedef double db;
#define mp(a,b) make_pair((a),(b))
#define x first
#define y second
#define be(a) (a).begin()
#define en(a) (a).end()
#define sz(a) int((a).size())
#define pb(a) push_back(a)
#define R(i,a,b) for(int i=(a),I=(b);i<I;i++)
#define L(i,a,b) for(int i=(a),I=(b);i>I;i--)
const int iinf=0x3f3f3f3f;
const ll linf=0x3f3f3f3f3f3f3f3f;

//Main
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    ll n,r1,r2,r3,d,ans=linf;
    cin>>n>>r1>>r2>>r3>>d;
    vector<ll> a(n),pa(n),st(n);
    R(i,0,n) cin>>a[i],pa[i]=r1*a[i]+r3,st[i]=min(r2,r1*(a[i]+1))+min(min(r1,r2),r3);
    vector<ll> f(n+1,linf),g(n+1); f[0]=d*(n-1);
    R(i,0,n){
        f[i+1]=min(f[i+1],f[i]+pa[i]);
        f[i+1]=min(f[i+1],f[i]+st[i]+d*2);
        if(i+1<n) f[i+2]=min(f[i+2],f[i]+st[i]+st[i+1]+d*2);
    }
    ans=min(ans,f[n]);
    L(i,n-2,-1) g[i]=g[i+1]+min(pa[i],st[i]);
    R(i,0,n-1){
        ans=min(ans,f[i]+g[i]+d*(n-1-i)+pa[n-1]);
        ans=min(ans,f[i]+g[i]+d*(n-1-i)+d*2+st[n-1]);
    }
    cout<<ans<<'\n';
    return 0;
}

---

祝大家学习愉快！