数字电路基础(三)TTL与非门输入端接电压表的示数
如下图所示,当ui输入低电平,电压表示数为0.3v,当ui输入高电平时,电压表示数为1.4v,分析如下
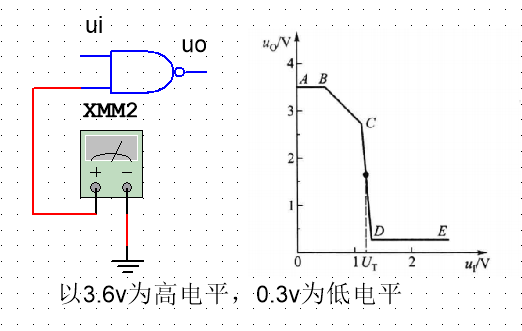
当ui=0.3
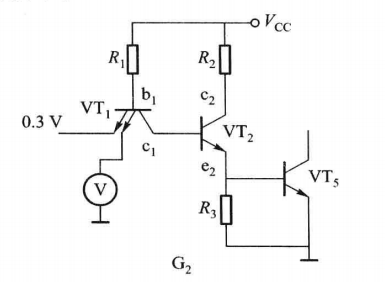
此时VT1导通,电流都从输入端流出,VT1的基极电位被钳位在1.0v(Ub1=0.3v+0.7v),那么电压表的示数就是1.0v-0.7v=0.3v。
当ui=3.6v
此时VT1的发射结反偏,属于截至状态,电流流向VT2,电压也都降落在VT2和VT5上,VT2和VT5导通,现在VT1的电位等于三个0.7v相加,即2.1v,此时电压表示数为2.1v-0.7v=1.4v。
所以在这里我觉得当考题不是只考逻辑的话,我们需要熟练掌握基本逻辑电路的电路原理,这样对自己掌握知识很有帮助,理解的也更透彻。
数字电路基础(三)TTL与非门输入端接电压表的示数的更多相关文章
- 数字电路基础(二)TTL与非门输入端悬空和接大电阻的问题
引言 我们在做那些判断与非门输入输出的时候,常常把输入端悬空和接大电阻作为高电平输入处理,比如下边这一例题: 很显然,我们无法直接从与非门逻辑图中看出其内部工作原理,那我们该如何分析呢?那肯定是去分析 ...
- TTL与非门电路的工作原理
分立元件门电路虽然结构简单,但是存在着体积大.工作可靠性差.工作速度慢等许多缺点.1961年美国德克萨斯仪器公司率先将数字电路的元器件和连线制作在同一硅片上,制成了集成电路.由于集成电路体积小.质量轻 ...
- TTL与非门电路分析
TTL与非门(TTL推挽式与非门)是TTL集成逻辑门的一种,主要由三极管和二极管构成.如图(a)所示,它由输入级,中间级,输出级三部分组成.TTL与非门的优点在于输出阻抗低,带负载能力强,工作速度快. ...
- FPGA入门到精通系列1:数字电路基础知识
本文主要介绍数字电路基础知识,用最简洁的内容介绍最核心的知识. 1.数字电路是什么? 数字电路是利用电源电压的高电平和低电平分别表示1和0,进而实现信息的表达.模拟信号:随时间连续变化的信号.处理 ...
- 数字电路基础知识——组合逻辑电路(数据选择器MUX、多路复用器)
转自:https://blog.csdn.net/vivid117/article/details/100747939 数字电路基础知识--组合逻辑电路(数据选择器MUX.也即多路复用器)本次介绍数据 ...
- Python全栈开发【基础三】
Python全栈开发[基础三] 本节内容: 函数(全局与局部变量) 递归 内置函数 函数 一.定义和使用 函数最重要的是减少代码的重用性和增强代码可读性 def 函数名(参数): ... 函数体 . ...
- day 53-1 Django基础三之视图函数
Django基础三之视图函数 本节目录 一 Django的视图函数view 二 CBV和FBV 三 使用Mixin 四 给视图加装饰器 五 Request对象 六 Response对象 一 Dja ...
- day 67 Django基础三之视图函数
Django基础三之视图函数 本节目录 一 Django的视图函数view 二 CBV和FBV 三 使用Mixin 四 给视图加装饰器 五 Request对象 六 Response对象 一 Dja ...
- Bootstrap <基础三十二>模态框(Modal)插件
模态框(Modal)是覆盖在父窗体上的子窗体.通常,目的是显示来自一个单独的源的内容,可以在不离开父窗体的情况下有一些互动.子窗体可提供信息.交互等. 如果您想要单独引用该插件的功能,那么您需要引用 ...
随机推荐
- RESTFUL风格的URL请求及参数接收
RESTFUL是一种网络应用程序的设计风格和开发方式,基于HTTP,可以使用XML格式定义或JSON格式定义.RESTFUL适用于移动互联网厂商作为业务使能接口的场景,实现第三方OTT调用移动网络资源 ...
- Redis好文章推荐
文章来源:掘金 作者:敖丙 Redis-避免缓存穿透的利器之BloomFilter <我们一起进大厂>系列- Redis基础 <我们一起进大厂>系列-缓存雪崩.击穿.穿透 ...
- [NewLife.Net]单机400万长连接压力测试
目标 对网络库NewLife.Net进行单机百万级长连接测试,并持续收发数据,检测网络库稳定性. [2020年8月1日晚上22点] 先上源码:https://github.com/NewLifeX/N ...
- Improving RGB-D SLAM in dynamic environments: A motion removal approach
一.贡献 (1)提出一种针对RGB-D的新的运动分割算法 (2)运动分割采用矢量量化深度图像 (3)数据集测试,并建立RGB-D SLAM系统 二.Related work [1]R.K. Namde ...
- Spring bean自定义命名策略(注解实现)
我们都知道项目后台开发是从 控制层——业务层——mybatis层,@Controller.@Service.@Mapper...等等注解可以将对象自动加载到bean容器中,还能实现相应的功能,使用起来 ...
- SpringMvc接收multipart/form-data 传输的数据 及 PostMan各类数据类型的区别
前段时间遇到一个问题,在spring mvc 服务端接收post请求时,通过html 表单提交的时候,服务端能够接收到参数的值.但是使用httpclient4.3构造post请求,却无法接收到参数的值 ...
- Focal Loss 损失函数简述
Focal Loss 摘要 Focal Loss目标是解决样本类别不平衡以及样本分类难度不平衡等问题,如目标检测中大量简单的background,很少量较难的foreground样本.Focal Lo ...
- CSS可见格式化模型
1.盒模型 1.1 盒子大小 盒模型描述了元素如何显示,以及如何相互作用.相互影响. 页面中的所有元素都被看作一个矩形盒子,这个盒子包含元素的内容.内边距.边框和外边距. 给元素应用的背景会作用于元素 ...
- ES6 面向对象笔记
JS面向对象两大编程思想 面向过程 面向对象 面向过程编程POP 面向过程就是分析出问题的需要步骤,然后用函数一步一步的实现,使用的时候一个一个调用就可以了 面向对象编程OOP ...
- java 的API及Object类
一 Java的API Java 的API(API: Application(应用) Programming(程序) Interface(接口)) Java API就是JDK中提供给我们使用的类,这些类 ...
