51Nod 1003 阶乘后面0的数量 | 思维
#include "bits/stdc++.h"
using namespace std;
#define LL long long
#define INF 0x3f3f3f3f3f
#define PI acos(-1)
#define N 510
LL arr[N];
int main()
{
int n,k;
while(~scanf("%d",&n)){
int sum=;
while(n>){
sum+=n/;
n/=;
}
printf("%d\n",sum);
}
return ;
}
51Nod 1003 阶乘后面0的数量 | 思维的更多相关文章
- 51Nod 1003 阶乘后面0的数量(数学,思维题)
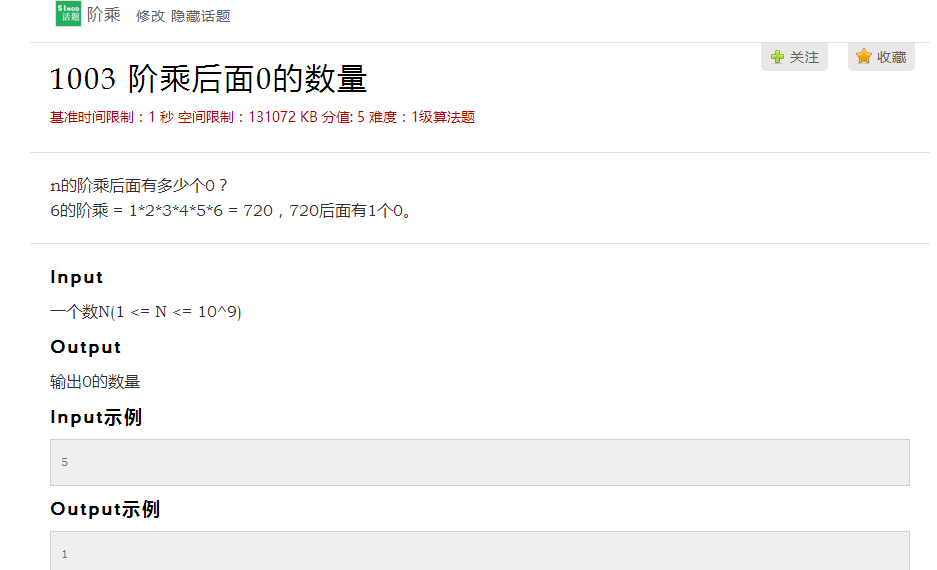
1003 阶乘后面0的数量 基准时间限制:1 秒 空间限制:131072 KB 分值: 5 难度:1级算法题 n的阶乘后面有多少个0? 6的阶乘 = 1*2*3*4*5*6 = 720 ...
- pku 1401 Factorial 算数基本定理 && 51nod 1003 阶乘后面0的数量
链接:http://poj.org/problem?id=1401 题意:计算N!的末尾0的个数 思路:算数基本定理 有0,分解为2*5,寻找2*5的对数,2的因子个数大于5,转化为寻找因子5的个数. ...
- 51nod 1003 阶乘后面0的数量
每一个 2 与一个 5 相乘,结果就增加一个零. 所以求 n! 后面的连续零的个数,其实就是求其中相乘的数含有因子每对因子 2 与 5 的个数. 又因为从1到某个数,所含 2 的个数比 5 多,所以 ...
- 51Nod:1003 阶乘后面0的数量
1003 阶乘后面0的数量 基准时间限制:1 秒 空间限制:131072 KB 分值: 5 难度:1级算法题 收藏 关注 n的阶乘后面有多少个0? 6的阶乘 = 1*2*3*4*5*6 = 72 ...
- 1001 数组中和等于K的数对 1002 数塔取数问题 1003 阶乘后面0的数量 1004 n^n的末位数字 1009 数字1的数量
1001 数组中和等于K的数对 基准时间限制:1 秒 空间限制:131072 KB 分值: 5 难度:1级算法题 给出一个整数K和一个无序数组A,A的元素为N个互不相同的整数,找出数组A中所有和等于K ...
- 51 Nod 阶乘后面0的数量
1003 阶乘后面0的数量 基准时间限制:1 秒 空间限制:131072 KB 分值: 5 难度:1级算法题 收藏 关注 n的阶乘后面有多少个0? 6的阶乘 = 1*2*3*4*5*6 = 72 ...
- (数学 尾0的个数) 51nod1003 阶乘后面0的数量
n的阶乘后面有多少个0? 6的阶乘 = 1*2*3*4*5*6 = 720,720后面有1个0. 收起 输入 一个数N(1 <= N <= 10^9) 输出 输出0的数量 输入样例 5 ...
- 51nod_1003 阶乘后面0的数量(求N!中5的个数,数论)
题意: n的阶乘后面有多少个0? 6的阶乘 = 1*2*3*4*5*6 = 720,720后面有1个0. Input 一个数N(1 <= N <= 10^9) OutPut 输出0的数 ...
- 51Nod 1003 1004 1009
1003 阶乘后面0的数量 基准时间限制:1 秒 空间限制:131072 KB 分值: 5 难度:1级算法题 n的阶乘后面有多少个0? 6的阶乘 = 1*2*3*4*5*6 = 720,720后面有1 ...
随机推荐
- LINUX监控一:监控命令
简单的整理一下常用的linux监控命令 本篇参考了:http://www.cnblogs.com/JemBai/archive/2010/07/30/1788484.html的内容 1.top top ...
- angularJS遇到的坑
最近在用angularjs做一些东西,由于学艺不精,对angularjs了解不够,导致经常会不小心掉进一些自己挖的坑里(⊙_⊙),在这里记下来,谨防又踩. 1.angularjs ng-show no ...
- Thunder团队第二周 - Scrum会议5
Scrum会议5 小组名称:Thunder 项目名称:爱阅app Scrum Master:苗威 工作照片: 参会成员: 王航:http://www.cnblogs.com/wangh013/ 李传康 ...
- 采用c#实现功能1
看了好多c#的菜鸟教程不如自己开始动手打代码,最终实现了功能一,参考了网上的wordcount代码发现无论是c++还是c#大部分采用的是哈希表的方法实现的,本来还想仅用循环实现遍历句子中的所有字符,即 ...
- C++读取文件统计单词个数及频率
1.Github链接 GitHub链接地址https://github.com/Zzwenm/PersonProject-C2 2.PSP表格 PSP2.1 Personal Software Pro ...
- vue项目怎么运行
因为要做毕业设计 ,准备用vue来做前端的界面.发现不知如何运行vue的项目,很尴尬.通过查阅网上教程,因此把环境搭建过程记录下来,以备不时之需. 言归正传~~ 首先,列出来我们需要的东西: ...
- isset、is_null、empty的区别
版本:PHP 5.4 1.isset() :检测变量是否存在,测试如下: $a = false; $b = null; $c; $d = 0; $e = true; var_dump(isset($a ...
- echarts 画 canvas 如果在IE8下不显示图标
网上说法很多,可能版本问题,也有说script标签位置问题(放在body中) 不过先试已下,清除option对象中多余的逗号(,) 对象的最后一个属性后不要有逗号结尾
- mac快速安装程序
homebrew:mac套件管理 官网 :http://brew.sh/index_zh-cn.html macport: 官网:https://www.macports.org/
- MATLAB中imfilter函数
功能:对任意类型数组或多维图像进行滤波. 用法:B = imfilter(A,H) B = imfilter(A,H,option1,option2,...) 或写作g = imfilter(f, w ...
