C++算法之旅、08 基础篇 | 质数、约数

质数

在>1的整数中，如果只包含1和本身这两个约数，就被称为质数(素数)

866 试除法判定

866. 试除法判定质数 - AcWing题库

\(O(n)\)

bool isprime(int x) {
    if (x < 2) return false;
    for (int i = 2; i < x; i++)
        if (x % i == 0) return false;
    return true;
}

约数 d 与 n / d 成对出现，可以枚举较小的那一个 \(O(\sqrt{n})\)

\(d <= n/d \\ d^2 <= n \\ d <= \sqrt{n}\)

难点

• 循环判断条件不要用 sqrt，每次循环都会执行一遍sqrt函数，比较慢
• 循环判断条件不要用 i * i，存在溢出风险（变成负数）
• 一定不会溢出的写法是 i <= n / i

#include <iostream>

using namespace std;

bool isprime(int n) {
    if (n < 2) return false;
    for (int i = 2; i <= n / i; i++)
        if (n % i == 0) return false;
    return true;
}

int main() {
    int n;
    cin >> n;
    while (n--) {
        int x;
        cin >> x;
        if (isprime(x))
            cout << "Yes" << endl;
        else
            cout << "No" << endl;
    }
}

867分解质因数

867. 分解质因数 - AcWing题库

质因数指能整除给定正整数的质数。把一个合数分解成若干个质因数的乘积的形式，即求质因数的过程叫做分解质因数。

相关理论证明可看 数论——质数：分解质因数 - 知乎 (zhihu.com)

从2到\(\sqrt{n}\)枚举n的所有质因数，求其指数并输出。还要考虑最多有一个质因素大于\(\sqrt{n}\)的情况，单独判断输出。 最坏 \(O(\sqrt{n})\)，最好 \(O(logn)\) (考虑\(2^k\)情况)

#include <iostream>

using namespace std;

void divide(int n) {
    for (int i = 2; i <= n / i; i++) {
        if (n % i == 0) {
            int cnt = 0;
            while (n % i == 0) {
                cnt++;
                n /= i;
            }
            cout << i << " " << cnt << endl;
        }
    }
    if (n > 1) cout << n << " " << 1 << endl;
}

int main() {
    int n;
    cin >> n;
    while (n--) {
        int x;
        cin >> x;
        divide(x);
        cout << endl;
    }
}

868筛质数

868. 筛质数 - AcWing题库

朴素算法是从前往后删倍数（2~p-1都不是n的约数，所以n是质数）

调和级数\(1/2+1/3+1/4+1/5+...+1/∞\) 极限等于 \(lnn+C\)。

\(lnn < log_2n\)，因此朴素算法复杂度为 \(O(nlogn)\)

埃式筛法：只删除2~p-1中质数的倍数，原理跟867类似（算数基本定理：每个正整数都可以唯一表示成素数的乘积）

粗略估计：1~n当中，有\(n/lnn\)个质数，时间复杂度变为 \(O(n)\)，真实复杂度 \(O(nloglogn)\)，两者差不多一个级别

#include <algorithm>
#include <iostream>

using namespace std;

const int N = 1e6 + 10;
int primes[N], cnt;
bool st[N];

void get_primes(int n) {
    for (int i = 2; i <= n; i++) {
        if (!st[i]) {
            primes[cnt++] = n;
            for (int j = i + i; j <= n; j += i) st[j] = true;
        }
    }
}

int main() {
    int n;
    cin >> n;
    get_primes(n);
    cout << cnt << endl;

    return 0;
}

线性筛法，\(O(n)\)，基本思路一样（基于每个质数的倍数为非质数），当 n 很大时，速度比埃式筛法快一倍。

每个数只会被其最小质因子筛掉

• i % pj == 0，pj 一定是 i 的最小质因子，pj 一定是 pj * i 的最小质因子
• i % pj != 0，pj 一定小于 i 的所有质因子，pj 一定是 pj * i 的最小质因子

#include <algorithm>
#include <iostream>

using namespace std;

const int N = 1e6 + 10;
int primes[N], cnt;
bool st[N];

void get_primes(int n) {
    for (int i = 2; i <= n; i++) {
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] * i <= n; j++) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;  // primes[j] 一定是 i 的最小质因子
        }
    }
}

int main() {
    int n;
    cin >> n;
    get_primes(n);
    cout << cnt << endl;

    return 0;
}

约数

869 试除法求约数

869. 试除法求约数 - AcWing题库

与866优化原理类似 \(O(\sqrt{n})\)

#include <algorithm>
#include <iostream>
#include <vector>

using namespace std;

vector<int> get_divisors(int n) {
    vector<int> res;
    for (int i = 1; i <= n / i; i++) {
        if (n % i == 0) {
            res.push_back(i);
            if (i != n / i) res.push_back(n / i);  // 避免平方
        }
    }
    sort(res.begin(), res.end());
    return res;
}

int main() {
    int n;
    cin >> n;
    while (n--) {
        int x;
        cin >> x;
        auto res = get_divisors(x);
        for (auto t : res) cout << t << ' ';
        cout << endl;
    }
}

870约数个数

利用算术基本定理，每个质因数有(1+n)种选择。m个选择组合得出m个约数

具体原理可看 第四章 数学知识（一）——质数与约数 - 知乎 (zhihu.com)

INT_MAX 约数个数约1500

870. 约数个数 - AcWing题库

求 n 个数的乘积的约数个数，可以求每个数的每个质因子指数之和，然后套用公式。

#include <algorithm>
#include <iostream>
#include <unordered_map>

using namespace std;

typedef long long LL;
const int mod = 1e9 + 7;

int main() {
    int n;
    cin >> n;
    unordered_map<int, int> primes;
    while (n--) {
        int x;
        cin >> x;
        for (int i = 2; i <= x / i; i++) {
            while (x % i == 0) {
                x /= i;
                primes[i]++;
            }
        }
        if (x > 1) primes[x]++;
    }
    LL res = 1;
    for (auto prime : primes) res = res * (prime.second + 1) % mod;
    cout << res << endl;
    return 0;
}

871约数之和

AcWing 871. 约数之和 - AcWing

#include <algorithm>
#include <iostream>
#include <unordered_map>

using namespace std;

typedef long long LL;
const int mod = 1e9 + 7;

int main() {
    int n;
    cin >> n;
    unordered_map<int, int> primes;
    while (n--) {
        int x;
        cin >> x;
        for (int i = 2; i <= x / i; i++) {
            while (x % i == 0) {
                x /= i;
                primes[i]++;
            }
        }
        if (x > 1) primes[x]++;
    }
    LL res = 1;
    for (auto prime : primes) {
        int p = prime.first, a = prime.second;
        LL t = 1;
        while (a--) {
            t = (t * p + 1) % mod;
        }
        res = res * t % mod;
    }
    cout << res << endl;
    return 0;
}

872最大公约数

872. 最大公约数 - AcWing题库

欧几里得算法（辗转相除法）

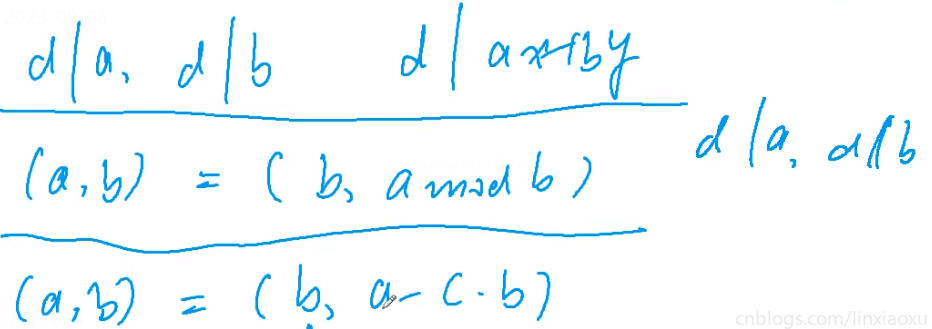
#include <algorithm>
#include <iostream>
#include <unordered_map>

using namespace std;

// a 和 0 的最大公约数是 a
int gcd(int a, int b) { return b ? gcd(b, a % b) : a; }

int main() {
    int n;
    cin >> n;
    while (n--) {
        int a, b;
        cin >> a >> b;
        cout << gcd(a, b) << endl;
    }
    return 0;
}