2023年多校联训NOIP层测试1

2023年多校联训NOIP层测试1

T1 luogu P6882 [COCI2016-2017#3] Imena \(50pts\)

• 赛场上被如何输入和判断是否合法薄纱了，赛后发现还有数字这一说，而且原题面也没看懂（还是我太拉了）。
• 打这题时把语音选成C了，然后 \(CE\) 困惑了我和@wangyunbiao 好一阵子。

  #include<bits/stdc++.h>
  using namespace std;
  #define ll long long
  #define sort stable_sort
  #define endl '\n'
  string s;
  int main()
  {
      int n,i,flag=0,ans=0,sum=0,len;
      cin>>n;
      while(sum<n)
      {
          cin>>s;//cin貌似读不进空格 利用这个进行读入
          flag=0;
          len=s.size();
          if('A'<=s[0]&&s[0]<='Z')
          {
              flag=1;
          }
          for(i=0;i<=len-1;i++)
          {
              if(i>=1)
              {
                  if('A'<=s[i]&&s[i]<='Z')//记得特判是否存在多个大写字母
                  {
                      flag=0;
                      break;
                  }
              }
              if('0'<=s[i]&&s[i]<='9')//如果有数字一定是不合法的
              {
                  flag=0;
                  break;
              }
          }
          if(flag==1)
          {
              ans++;
          }
          if(s[len-1]=='.'||s[len-1]=='?'||s[len-1]=='!')//如果到达末尾就输出
          {
              cout<<ans<<endl;
              ans=flag=0;
              sum++;
          }
      }
      return 0;
  }
  

T2 COCI 2016/2017 Round #3 Pohlepko \(6pts\)

• 400w的string用来记录每条路径的结果可真有我的，成功 \(MLE\) 。
• 分析样例，易知正方形对角线上的点横纵坐标之和相等，例如对角线②上的点横纵坐标之和为 \(2+1=1+2=3\) ,对角线③上的点横纵坐标之和为 \(3+1=2+2=1+3=4\) 。
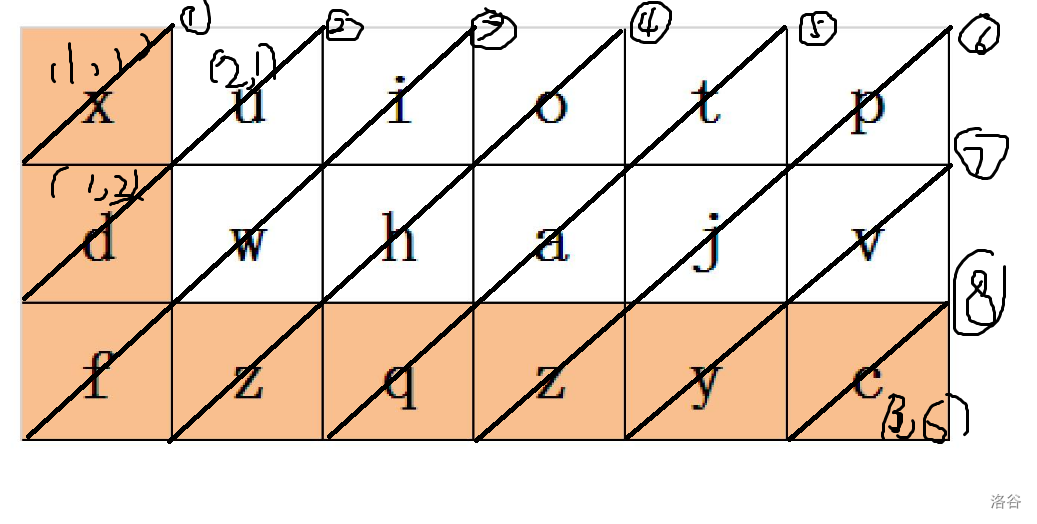
• 由 \((1,1)\) 到达 \((n,m)\) 易证需要经过 \(n+m-1\) 个点。
• 考虑枚举第 \(i (2≤i≤n+m-1)\) 条对角线，遍历点 \((j,i-j+1)\) ，判断上个点( \((j-1,i-j+1) or (j,i-j)\) )是否可进行扩展，即能到达点 \((j,i-j+1)\) ，并于其中选出字典序最小的（如果有多个则都进行标记，直到找到相对唯一最小的或到达终点），标记这些位置是可进行扩展的。

  #include<bits/stdc++.h>
  using namespace std;
  #define ll long long
  #define sort stable_sort
  #define endl '\n'
  char a[2001][2001],minn;
  int vis[2001][2001];//vis[x][y]用来记录点(x,y)是否可以进行扩展
  int main()
  {
      int n,m,i,j,k;
      cin>>n>>m;
      for(i=1;i<=n;i++)
      {
          for(j=1;j<=m;j++)
          {
              cin>>a[i][j];
          }
      }
      cout<<a[1][1];
      vis[1][1]=1;
      for(i=2;i<=n+m-1;i++)//枚举对角线
      {
          minn='z';
          for(j=1;j<=n;j++)//枚举点
          {
              k=i+1-j;
              if(1<=k&&k<=m)//判断点是否合法
              {
                  if(vis[j-1][k]==1)//找到最小值
                  {
                      minn=min(minn,a[j][k]);
                  }
                  if(vis[j][k-1]==1&&a[j][k]<minn)//找到最小值
                  {
                      minn=min(minn,a[j][k]);
                  }
              }
          }
          cout<<minn;//输出最小字母
          for(j=1;j<=n;j++)
          {
              k=i+1-j;
              if(1<=k&&k<=m)
              {
                  if(vis[j-1][k]==1&&a[j][k]==minn)//进行扩展
                  {
                      vis[j][k]=1;
                  }
                  if(vis[j][k-1]==1&&a[j][k]==minn)//进行扩展
                  {
                      vis[j][k]=1;
                  }
              }
          }
      }
      return 0;
  }
  

T3 luogu P7535 [COCI2016-2017#4] Kas \(15pts\)

• 发现这道题和学校oj上某年CSP-J模拟赛T2很像,不过那道题要求差值尽可能小，故令 \(sum=\sum\limits_{i=1}^{n} v[i]\) ，构建容量为 \(\frac{sum}{2}\) 的 \(01\) 背包，且每件物品的质量和价值相等（即 \(w[i]=v[i]\) )。但本题要求差值为 \(0\) 。
• 考虑 \(DP\) ，令 \(f[i][j]\) 表示前 \(i\) 张钞票分给两人后满足差值为 \(j\) 的最大总金额（不用管如何分配，赛场上因为这个考虑太多所以祭了）。
  • 然后当遍历到第 \(i\) 张钞票进行分类讨论：
    • 第 \(i\) 张钞票两人都不给，此时有 \(f[i][j]=f[i-1][j]\) 。
    • 将第 \(i\) 张钞票给两人中金额少的那人，此时有 \(f[i][j]=max(f[i][j],f[i-1][j+a[i]]+a[i])\) 。
    • 将第 \(i\) 张钞票给两人中金额多的那人，此时有 \(f[i][j]=max(f[i][j],f[i-1][abs(j-a[i])]+a[i])\) 。
      • 注意是 \(abs(j-a[i])\) ,因为原来的差值可能是 \(j-a[i]\) ,也可能是 \(a[i]-j\) 。
  • 得到 \(DP\) 式子， \(f[i][j]=max\lbrace f[i-1][j],f[i-1][j+a[i]]+a[i],f[i-1][abs(j-a[i])]+a[i]\rbrace\) 。
    • 因为转移第一维时仅需要从上一维进行转移，可以加滚动数组优化，以此达到时间换空间的做法。
  • 代码

    //不加滚动数组
    #include<bits/stdc++.h>
    using namespace std;
    #define ll long long
    #define sort stable_sort
    #define endl '\n'
    int a[502],f[502][100002];
    int main()
    {
        int n,i,j,sum=0;
        cin>>n;
        memset(f,-0x3f,sizeof(f));//给f数组赋一个很小的值
        f[0][0]=0;
        for(i=1;i<=n;i++)
        {
            cin>>a[i];
            sum+=a[i];
        }
        for(i=1;i<=n;i++)
        {
            for(j=0;j<=sum;j++)
            {
                f[i][j]=max(f[i-1][j],max(f[i-1][j+a[i]]+a[i],f[i-1][abs(j-a[i])]+a[i]));
            }
        }
        cout<<sum-f[n][0]+f[n][0]/2;//(sum-f[n][0])*2/2+f[n][0]/2
        return 0;
    }
    

    //使用滚动数组
    #include<bits/stdc++.h>
    using namespace std;
    #define ll long long
    #define sort stable_sort
    #define endl '\n'
    int a[502],f[100002],g[100002];
    int main()
    {
        int n,i,j,sum=0;
        cin>>n;
        memset(f,-0x3f,sizeof(f));
        f[0]=0;
        for(i=1;i<=n;i++)
        {
            cin>>a[i];
            sum+=a[i];
        }
        for(i=1;i<=n;i++)
        {
            for(j=0;j<=sum;j++)
            {
                g[j]=max(f[j],max(f[j+a[i]]+a[i],f[abs(j-a[i])]+a[i]));//取一个g数组用来临时存储转移结果
            }
            for(j=0;j<=sum;j++)
            {
                f[j]=g[j];
            }
        }
        cout<<sum-f[0]+f[0]/2;
        return 0;
    }
    

T4 CF1301F Super Jaber \(10pts\)

• 赛场上咕了，暴力建边，跑了一遍 \(Floyd\) ，骗了 \(10pts\) ，就去弄别的了。骗分代码
• 题面翻译得不太好，包括但不限于“并排相邻”，明显机翻痕迹。
• 考虑记录同种颜色的点的坐标，然后跑 \(BFS\) 处理多源最短路。
  • 把相同颜色的点看做一个传送门。
  • 令 \(dis[i][x][y]\) 表示以颜色为 \(i\) 的任意非 \((x,y)\) 点作为起点到达 \((x,y)\) 的最小距离，并开一个 \(vis\) 数组标记是否走过。
  • 接着跑 \(BFS\) 预处理，实现 \(O(1)\) 查询。
  • 时间复杂度 \(O(nm+nmk+qk)\) ，卡常代码（注释也在这里）。
• \(CF\) 上时限 \(5s\) ,不卡常代码跑到了 \(4.5s\) ，所以"略带"卡常，然后就手写了 \(queue\) ，加上了火车头和快读(请使用 C++11 或更高的版本编译)， \(i++\) 改成了 \(++i\) ，尽量减少对数组的调用及变量重复定义消耗的时间，使用 \(bool\) 代替 \(int\) ，在主函数内使用 \(register \ int\) 。
  • 卡常跑进 \(0.96s\) 以内了，有更优卡常方法@我。
  • 
  • 代码（把快读快写部分删了）

    #include<bits/stdc++.h>
    using namespace std;
    #define ll long long
    #define sort stable_sort
    #define endl '\n'
    struct sx_queue//手写队列
    {
        int q[2000000],l=1,r=1;
        inline void push(int x){q[++r]=x;}
        inline int front(){return q[l+1];}
        inline void pop(){++l;}
        inline int back(){return q[r];}
        inline int size(){return r-l;}
        inline bool empty(){return l>=r;}
    };
    int main()
    {
        int n,m,k,q,nx,ny,r1,c1,r2,c2,ans,lsx,lsy,lsc,i,j;
        cin(n,m,k);
        for(i=1;i<=n;++i)
        {
            for(j=1;j<=m;++j)
            {
                cin(color[i][j]);
                ++sum[color[i][j]];
                x[color[i][j]].push_back(i);
                y[color[i][j]].push_back(j);
            }
        }
        for(i=1;i<=k;++i)
        {
            sx_queue qx,qy;
            memset(vis,false,sizeof(vis));
            vis[i]=true;
            for(j=0;j<sum[i];++j)
            {
                qx.push(x[i][j]);
                qy.push(y[i][j]);
                dis[i][x[i][j]][y[i][j]]=1;
            }
            while(!qx.empty())//跑一遍BFS
            {
                lsx=qx.front();
                qx.pop();
                lsy=qy.front();
                qy.pop();
                for(j=0;j<=3;++j)
                {
                    nx=dir[j][0]+lsx;
                    ny=dir[j][1]+lsy;
                    if(1<=nx&&nx<=n&&1<=ny&&ny<=m&&(!dis[i][nx][ny]))//这里用来处理颜色连通情况
                    {
                        qx.push(nx);
                        qy.push(ny);
                        dis[i][nx][ny]=dis[i][lsx][lsy]+1;
                    }
                }
                lsc=color[lsx][lsy];
                if(!vis[lsc])
                {
                    vis[lsc]=true;
                    for(j=0;j<sum[lsc];++j)
                    {
                        if(!dis[i][x[lsc][j]][y[lsc][j]])
                        {
                            qx.push(x[lsc][j]);
                            qy.push(y[lsc][j]);
                            dis[i][x[lsc][j]][y[lsc][j]]=dis[i][lsx][lsy]+1;
                        }
                    }
                }
            }
        }
        cin(q);
        for(i=1;i<=q;++i)
        {
            cin(r1,c1,r2,c2);
            ans=abs(r2-r1)+abs(c2-c1);//如果不经过传送门，易知结果为两点的曼哈顿距离
            for(j=1;j<=k;++j)
            {
                ans=min(ans,dis[j][r1][c1]+dis[j][r2][c2]-1);//-1是因为重复计算一个点
            }
            cout(ans,'\n');
        }
        return 0;
    }
    

总结

看清语言再提交。