Google的TPU的逐元素操作特性 —— TPU数据操作时最基本的操作原语(primitive)

地址：

https://jax.readthedocs.io/en/latest/pallas/tpu.html

TPU是原来进行矩阵计算加速的一个科学计算的设备，功能大致等同于NVIDIA的GPU的CUDA，但是功能上要更少，对矩阵计算能力更强。

TPU对数据进行运算时是存在基本操作的，如加、减、乘、除、赋值、取反.....，其他的对矩阵进行的操作都可以在这里操作之上进行构建，比如：relu操作就可以在比较操作和jnp.where操作基础上进行组合构建。

以下给出TPU的对数据元素的最基本的操作原语：

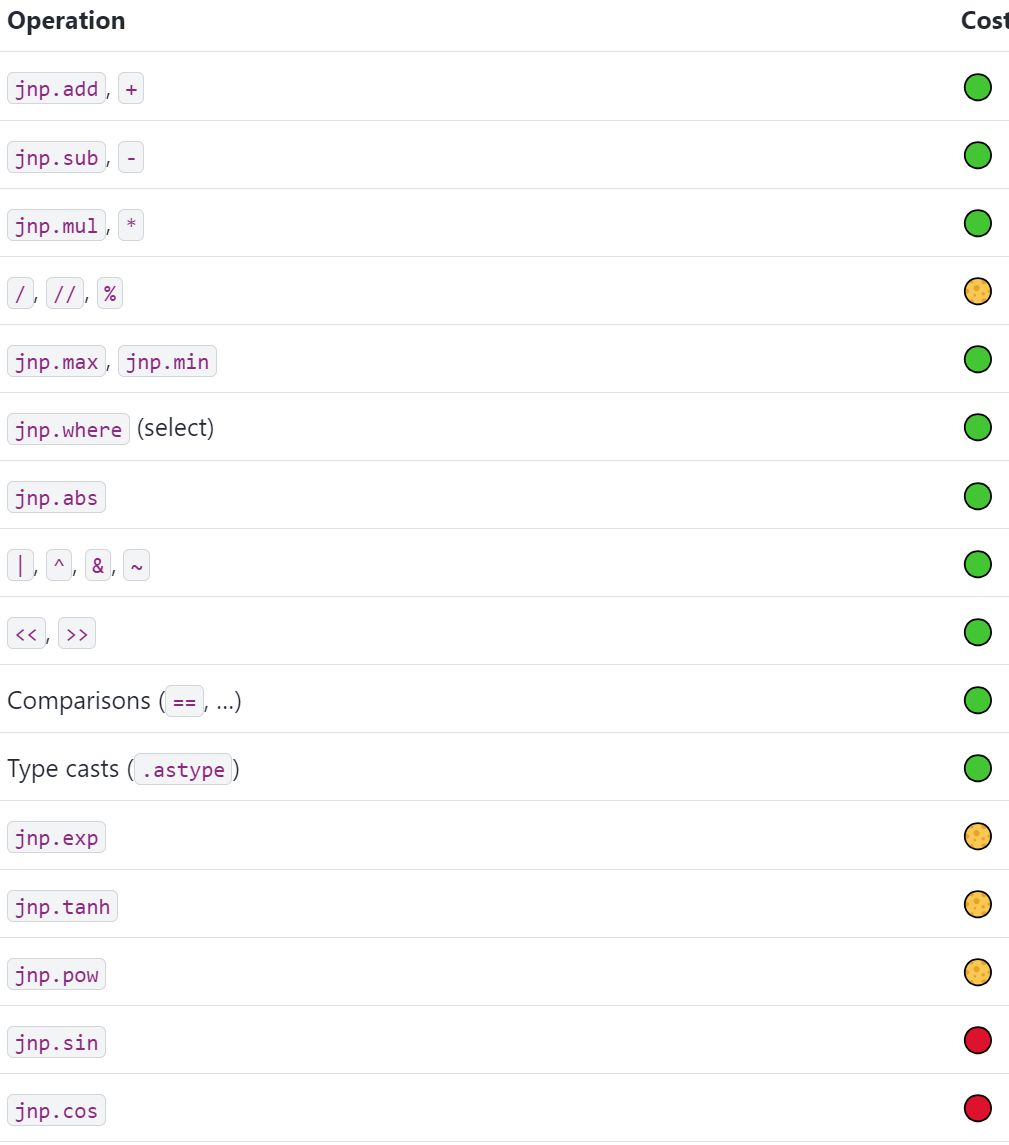
PS. 红色的标记代表运算难度最大，也是最耗时的。可以看到，比较操作、基础运算操作、位运算操作都是比较快速的，exp、tanh、pow操作会更加耗时，最耗时的是三角运算操作。

TPU是ASIC类型设备，因此基本的元素操作都是利用硬件电路来实现的，因此ASIC的数据操作的速度是要高于GPU这种通用计算设备的，并且耗能更低。