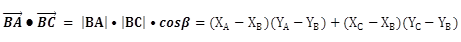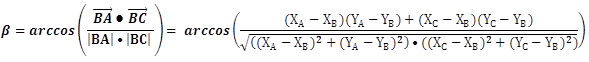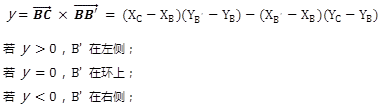C#多边形求角——实例说

前段时间有写过一个计算多边形角度的代码，这里给它整理整理，留给自己也送给萌新。

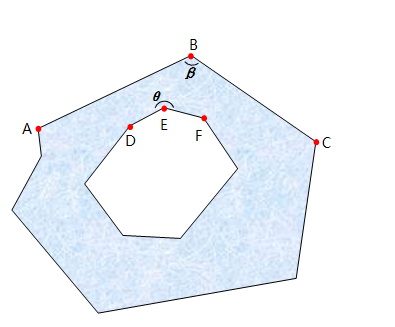
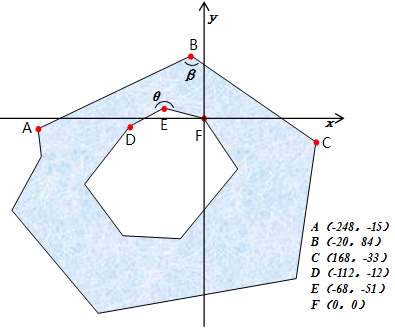
看左下图，这是一个多环的多边形，一个外环（内部为多边形内部区域），一个内环（外部为多边形内部区域），同时多边形中任意一个角不等于零角（等于 0° 的角）或周角（等于 360° 的角）。注意：本文下文所讨论的多边形求角度不包含零角和周角。

现在我们要求 ∠ABC 和 ∠DEF 的大小。那咋算唻?

---

1. 内积计算夹角

给它加上坐标系（坐标是自己配的，计算出的角度值不一定准确，但不影响角度大小的关系）， 如右上图。角度采用向量的内积来求。

以上面的 ∠ABC 为例，数学计算公式如下。

于是乎，有：

角度计算代码如下：

public struct CxPoint
{
    public CxPoint(double x, double y)
    {
        X = x;
        Y = y;
    }

    public double X;
    public double Y;
}

/// <summary>
/// 计算三点角度，p1-p2-p3为沿环方向的三个连续顶点，其中p2为角点。计算结果范围 0° - 180°，-1为无效值
/// </summary>
private static double CalculationAngle(CxPoint p1, CxPoint p2, CxPoint p3)
{
    //Cos(Angle) =  a•b/(|a|*|b|)
    double x1 = p1.X - p2.X, y1 = p1.Y - p2.Y;  //向量 a
    double x2 = p3.X - p2.X, y2 = p3.Y - p2.Y;  //向量 b

    //零向量，存在共点
    if (x1 ==  && y1 == ) return -;
    if (x2 ==  && y2 == ) return -;

    double v = x1 * x2 + y1 * y2;   //向量内积 a•b
    double val = Math.Sqrt((x1 * x1 + y1 * y1) * (x2 * x2 + y2 * y2));  //a,b模长乘积 |a|*|b|
    double CosAngle = v / val;  //求出来的值可能略小于 -1 或者略大于 1，此时 Angle 等于 NaN
    double Angle = Math.Acos(CosAngle) * 180.0 / 3.14159265358979;  //两向量夹角，0-180

    if (System.Double.IsNaN(Angle))
    {
        if (v > ) return ;
        else return ;
    }
    else
    {
        if (Angle > ) return ;
        else if (Angle < ) return ;
        else return Angle;
    }
}

参考代码

用上述代码我们能够计算得出 ∠ABC = 124.63°，∠DEF = 101.57°。细心的朋友会发现，∠DEF 很明显是个优角（大于 180° 小于 360° 的角），为什么求出来是个劣角的值（大于 0° 小于 180° 的角）呢？原来反余弦函数的值域为 [ 0，π ]，故采用向量内积计算出来的夹角总是在 [ 0°，180° ] 之间。

---

2. 外积判断互组

针对像 ∠DEF 这种优角，我们如何计算其结果呢？原来，内积计算的夹角与正确结果必定互为组角（相加等于 360° 的两个角互为组角），如此 ∠DEF 的正确结果为 360° - 101.57° = 258.43°。故在内积计算夹角后，问题转换为判别待求角是优角还是劣角，优角则求其组角，劣角则直接是结果。

以 ∠ABC 为例 ，A → B → C 为环方向，取AC中点M，再取 BM 上靠近 B 点的 B' 点（称为面内面外判断点），其中 BB' 的距离很小很小（若直接以 M 点作为面内面外判断点，由于存在多环的情况，会出现问题）。若 B' 在多边形内，则待求角为劣角，内积计算夹角即为结果，若 B' 在多边形外，即出现 ∠DEF 这种情况（此时 B' 是 E'）,则需要求内积计算夹角的组角作为计算结果。

面内面外判断点求取代码如下：

/// <summary>
/// 求取面内面外判断点，p1-p2-p3为沿环方向的三个连续顶点，其中p2为角点。
/// </summary>
private static CxPoint CalculationJudgePoint(CxPoint p1, CxPoint p2, CxPoint p3, double SmallDis = 0.01)
{
    double TempX = (p1.X + p3.X) / ;
    double TempY = (p1.Y + p3.Y) / ;

    double DisX = TempX - p2.X;
    double DisY = TempY - p2.Y;
    double val = Math.Sqrt(DisX * DisX + DisY * DisY);

    double Scale = SmallDis / val;

    return new CxPoint(p2.X + Scale * DisX, p2.Y + Scale * DisY);
}

参考代码

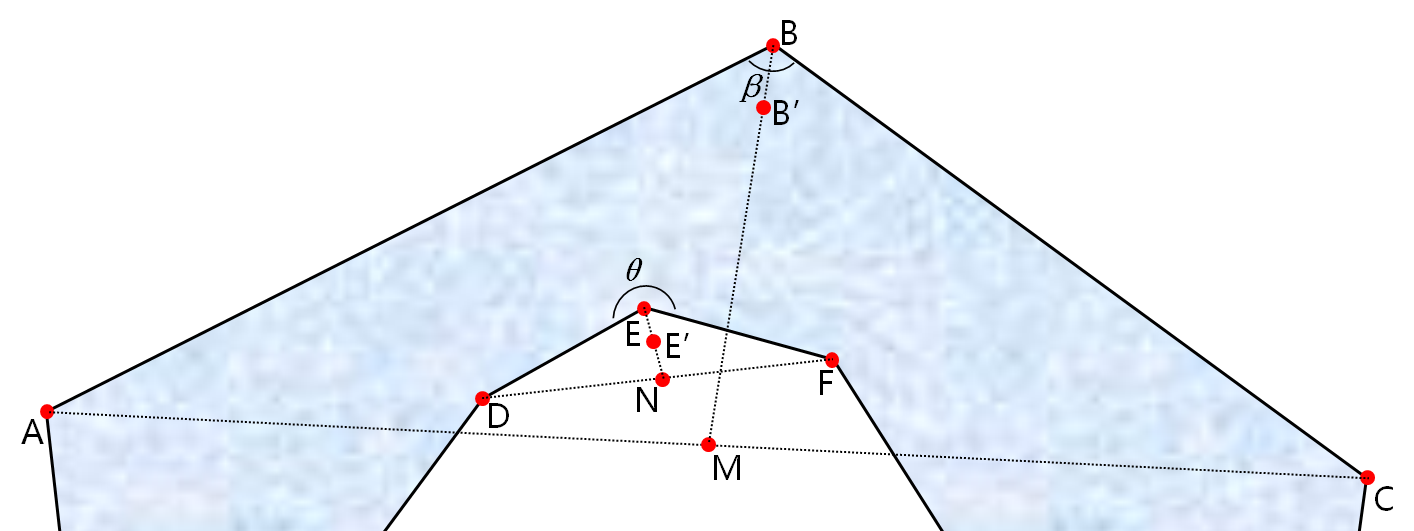
假设，沿着环的方向，多边形的内部总在环的右侧区域，所以在上图中，∠ABC 所在的环为顺时针方向，∠DEF 所在的环为逆时针方向。有了这个假设，我们就能够用向量外积来判断 B' （或者是 E'）点是否在面内了。具体做法为计算 ( 待求角角点，沿环方向角点下一顶点 ) 与 ( 待求角角点，面内面外判断点 ) 的外积（在本文图中为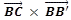和 ）：结果若大于 0，则面内面外判断点在环的左侧和多边形外部，待求角为优角，求内积计算夹角的组角作为结果；结果若小于等于 0，则面内面外判断点在环的右侧和多边形内部或边界上，待求角为劣角或平角，内积计算夹角直接作为结果。

以判断 B' 在 BC 的哪一侧为例，数学计算公式如下。

左右侧判断代码如下：

public struct CxLine
{
    public CxLine(CxPoint fromPoint, CxPoint toPoint)
    {
        FromPoint = fromPoint;
        ToPoint = toPoint;
    }

    public CxPoint FromPoint;
    public CxPoint ToPoint;
}

/// <summary>
/// 判断点在线的左方还是右方，在左为 true，在线上或在右为 false
/// </summary>
public static bool JudgAbout(CxLine pLine, CxPoint pPoint)
{
    double ax = pLine.ToPoint.X - pLine.FromPoint.X;
    double ay = pLine.ToPoint.Y - pLine.FromPoint.Y;
    double bx = pPoint.X - pLine.FromPoint.X;
    double by = pPoint.Y - pLine.FromPoint.Y;
    double judge = ax * by - ay * bx;

    if (judge > 0.0)
        return true;
    else
        return false;
}

参考代码

---

3. 求角源码整理

通过上述分析，将所有代码整理成一个 cs 类。

/// <summary>
    /// 调用示例：AngleCalculation.CxPoint p1 = new AngleCalculation.CxPoint(-112, -12);
    ///           AngleCalculation.CxPoint p2 = new AngleCalculation.CxPoint(-68, -51);
    ///           AngleCalculation.CxPoint p3 = new AngleCalculation.CxPoint(0, 0);
    ///           double angle = AngleCalculation.Analysis(p1, p2, p3, true);
    /// </summary>
    public sealed class AngleCalculation
    {
        public struct CxPoint
        {
            public CxPoint(double x, double y)
            {
                X = x;
                Y = y;
            }

            public double X;
            public double Y;
        }

        public struct CxLine
        {
            public CxLine(CxPoint fromPoint, CxPoint toPoint)
            {
                FromPoint = fromPoint;
                ToPoint = toPoint;
            }

            public CxPoint FromPoint;
            public CxPoint ToPoint;
        }

        /// <summary>
        /// 角度计算主方法，p1-p2-p3为沿环方向的三个连续顶点，其中p2为角点。
        /// </summary>
        /// <param name="IsClockwise">p1-p2-p3所在环方向，顺时针为 true，逆时针为 false</param>
        public static double Analysis(CxPoint p1, CxPoint p2, CxPoint p3, bool IsClockwise)
        {
            double Angle = CalculationAngle(p1, p2, p3);
            if (Angle == -) return Angle;

            CxPoint JudgePoint = CalculationJudgePoint(p1, p2, p3);
            CxLine ReferenceLine = new CxLine(p2, p3);

            bool IsLeft = JudgAbout(ReferenceLine, JudgePoint);

            if (IsClockwise == IsLeft) Angle =  - Angle;

            return Angle;
        }

        /// <summary>
        /// 计算三点角度，p1-p2-p3为沿环方向的三个连续顶点，其中p2为角点。计算结果范围 0° - 180°，-1为无效值
        /// </summary>
        private static double CalculationAngle(CxPoint p1, CxPoint p2, CxPoint p3)
        {
            //Cos(Angle) =  a•b/(|a|*|b|)
            double x1 = p1.X - p2.X, y1 = p1.Y - p2.Y;  //向量 a
            double x2 = p3.X - p2.X, y2 = p3.Y - p2.Y;  //向量 b

            //零向量，存在共点
            if (x1 ==  && y1 == ) return -;
            if (x2 ==  && y2 == ) return -;

            double v = x1 * x2 + y1 * y2;   //向量内积 a•b
            double val = Math.Sqrt((x1 * x1 + y1 * y1) * (x2 * x2 + y2 * y2));  //a,b模长乘积 |a|*|b|
            double CosAngle = v / val;  //求出来的值可能略小于 -1 或者略大于 1，此时 Angle 等于 NaN
            double Angle = Math.Acos(CosAngle) * 180.0 / 3.14159265358979;  //两向量夹角，0-180

            if (System.Double.IsNaN(Angle))
            {
                if (v > ) return ;
                else return ;
            }
            else
            {
                if (Angle > ) return ;
                else if (Angle < ) return ;
                else return Angle;
            }
        }

        /// <summary>
        /// 求取面内面外判断点，p1-p2-p3为沿环方向的三个连续顶点，其中p2为角点。
        /// </summary>
        private static CxPoint CalculationJudgePoint(CxPoint p1, CxPoint p2, CxPoint p3, double SmallDis = 0.01)
        {
            double TempX = (p1.X + p3.X) / ;
            double TempY = (p1.Y + p3.Y) / ;

            double DisX = TempX - p2.X;
            double DisY = TempY - p2.Y;
            double val = Math.Sqrt(DisX * DisX + DisY * DisY);

            double Scale = SmallDis / val;

            return new CxPoint(p2.X + Scale * DisX, p2.Y + Scale * DisY);
        }

        /// <summary>
        /// 判断点在线的左方还是右方，在左为 true，在线上或在右为 false
        /// </summary>
        private static bool JudgAbout(CxLine pLine, CxPoint pPoint)
        {
            double ax = pLine.ToPoint.X - pLine.FromPoint.X;
            double ay = pLine.ToPoint.Y - pLine.FromPoint.Y;
            double bx = pPoint.X - pLine.FromPoint.X;
            double by = pPoint.Y - pLine.FromPoint.Y;
            double judge = ax * by - ay * bx;

            if (judge > 0.0)
                return true;
            else
                return false;
        }
    }
}

参考代码

 

作者：喵...鱼...喵

出处：https://www.cnblogs.com/bwuwj/

本文为作者原创，版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文链接，否则保留追究法律责任的权利。如本文有误，欢迎批评指正。