Codeforces 848E - Days of Floral Colours（分治 FFT）

Codeforces 题目传送门 & 洛谷题目传送门

神仙 D1E，一道货真价实的 *3400 %%%%%%%%%%%%

首先注意到一点，由于该图为中心对称图形，\(1\sim n\) 的染色情况一定与 \(n+1\sim 2n\) 的染色情况完全相同，也就是说我们只需考虑 \(1\sim n\) 的染色情况，\(n+1\sim 2n\) 部分各段的长度一定与 \(1\sim n\) 部分的长度完全相同，权值平方一下即可。

我们不妨假设 \(1\) 与 \(n+1\) 之间连了一条长度为 \(n\) 的边，当然这边有人会担心 \(1\) 与 \(n+1\) 之间如果不存在长度为 \(n\) 的边怎么办，事实上我们可以将其旋转一个角度，这样就可以归约到 \(1\) 与 \(n+1\) 之间存在边的情况了，具体细节将在最后提到。

我们设 \(dp_i\) 为已经确定了花朵 \(1\sim i\) 的连边方式，并且 \(i\) 与 \(i+n\) 之间连了一条长度为 \(n\) 的边的情况下，所有方案的权值之和，考虑转移，简单画个图就可以发现对于任意一对存在边的花朵，可能的图形只有以下四种（这里蒯了神仙 \(\color{black}\texttt{s}\color{red}\texttt{hadowice1984}\) 神仙题解里的图：

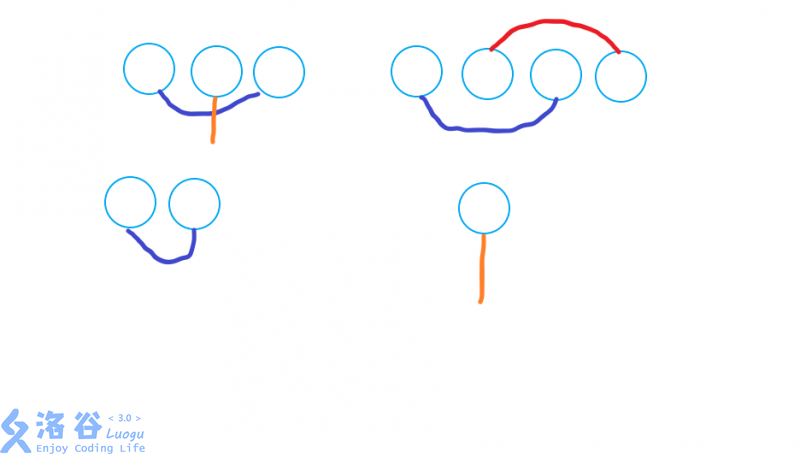
稍微解释一下上面这张图，这四幅图分别对应以下四种情况：

• 花朵 \(i\) 与花朵 \(i+n\) 连长度为 \(n\) 的边（即右下角的图）
• 花朵 \(i\) 与花朵 \(i+1\) 连长度为 \(1\) 的边（即左下角的图）
• 花朵 \(i\) 与花朵 \(i+2\) 连长度为 \(2\) 的边，同时花朵 \(i+1\) 与花朵 \(i+3\) 也连长度为 \(2\) 的边（即右上角的图）
• 花朵 \(i\) 与花朵 \(i+2\) 连长度为 \(2\) 的边，同时花朵 \(i+1\) 与花朵 \(i+n+1\) 连长度为 \(n\) 的边（即左上角的图）

前面三种情况都异常容易解决。为了表述方便，我们定义连续段为极长的不存在连了长度为 \(n\) 的边的花朵段，记连续段的长度为这个连续段中花朵的个数 \(+1\)，那么长度为 \(m\) 的连续段的权值就是 \((m-1)^2\)。记 \(g_i\) 为长度为 \(i\) 的连续段连边的方案数，那么显然有递推式 \(g_i=g_{i-2}+g_{i-4}\)，\(g_0=1\)。预处理 \(g\) 数组之后就可以枚举上一段长度为 \(n\) 的边的位置转移了，即 \(dp_i=\sum\limits_{j=1}^{i-1}dp_jg_{i-j}(i-j-1)^2\)。

繁琐的地方在于最后一种情况，也就是长度为 \(n\) 的边的两边存在长度为 \(2\) 的边的情况。在下文中为了表述方便我们记这种图形为特殊图形。显然加上这种情况之后原来的 \(dp\) 状态就不可行了，因为最后一段存在特殊图形与不存在特殊图形的转移是不同了，此时我们就要在 \(dp\) 状态中引入常数项来区分存在特殊图形与不存在特殊图形的情况。具体来说，对于一个长度为 \(m\) 的连续段，它内部特殊图形的存在情况只可能有四种情况（*）：

• 左右部分都不存在特殊图形
• 左边存在特殊图形，右边不存在特殊图形
• 左边不存在特殊图形，右边存在特殊图形
• 左右部分都存在特殊图形

不难发现第一种情况的方案数就是 \(g_{m-1}\)，第二、三种情况是等价的，方案数都是 \(g_{m-2}\)，因为有一朵花的方案已经确定了，只能在剩余 \(m-2\) 朵花中配对，同理第四种情况方案数是 \(g_{m-3}\)。

了解了这一点之后，我们的方向就明确了。我们在 \(dp\) 状态中新增一维常数，即将原来的 \(dp\) 状态更改为 \(dp_{i,0/1/2}\)，表示当前考虑到了第 \(i\) 朵花，并且第 \(i\) 朵花连了长度为 \(n\) 的边，第 \(1\) 朵花与第 \(n\) 朵花周围总共有 \(0/1/2\) 个特殊图形的方案的贡献之和，那么有转移：

• \(dp_{i,0}=g_{i-1}(i-1)^2+\sum\limits_{j=1}^{i-1}dp_{i-j,0}(i-1)^2g_{i-1}+\sum\limits_{j=1}^{i-1}dp_{i-j,1}(i-1)^2g_{i-2}\)
• \(dp_{i,1}=g_{i-2}(i-1)^2+\sum\limits_{j=1}^{i-1}dp_{i-j,0}(i-1)^2g_{i-2}+\sum\limits_{j=1}^{i-1}dp_{i-j,1}(i-1)^2g_{i-3}\)
• \(dp_{i,2}=g_{i-3}(i-1)^2+\sum\limits_{j=1}^{i-1}dp_{i-j,1}(i-1)^2g_{i-2}+\sum\limits_{j=1}^{i-1}dp_{i-j,2}(i-1)^2g_{i-3}\)

稍微解释一下上面的 \(dp\) 转移方程。在 \(dp_{i,0}\) 的转移方程中，前面 \(g_{i-1}(i-1)^2\) 表示 \(1\sim i\) 这 \(i\) 个花朵本身就形成了一个长度为 \(i\) 的连续段，贡献为 \(g_{i-1}(i-1)^2\)，否则我们就枚举上一段连续段的长度 \(j\)，并分上一个连了长度为 \(n\) 的地方的边出不出现特殊图形两种情况进行转移，如果不出现那就从 \(dp_{i-j,0}\) 转移过来，方案数同（*）处的第一种情况，为 \(g_{i-1}\)，再乘上本次划分的贡献 \((i-1)^2\)，如果出现那就从 \(dp_{i-j,1}\) 转移过来，方案数同（*）处的第二种情况，为 \(g_{i-2}\)，因此我们有 \(dp_{i,0}=g_{i-1}(i-1)^2+\sum\limits_{j=1}^{i-1}dp_{i-j,0}(i-1)^2g_{i-1}+\sum\limits_{j=1}^{i-1}dp_{i-j,1}(i-1)^2g_{i-2}\)，\(dp_{i,1},dp_{i,2}\) 的转移方程也同理，自己稍微推推应该可以推出来。这样暴力转移是平方的，不过注意到这样的 \(dp\) 转移方程满足 \(f_{i}=\sum f_{i-j}g_j\) 的形式（我 卷 我 自 己），因此考虑分治 FFT 优化，复杂度 \(n\log^2n\)，当然也可以多项式求逆，复杂度少一个 \(\log\)，这里就不赘述了。

最后考虑怎样计算答案，分三种情况：

• 如果不存在长度为 \(n\) 的边，这样可能会有一些情况，不过反正贡献都是 \(0\)，你还管那么多干嘛呢（
• 如果存在一条长度为 \(n\) 的边，那考虑枚举这条边的一个端点 \(i(i\le n)\)，不妨设 \(1\) 为这条边的一个端点，最后乘个 \(n\) 即可。分两种情况，要么 \(1\) 和 \(n+1\) 两边都存在特殊图形，要么都不存在，根据对称性不可能存在一遍有特殊图形一边没有的情况。前者方案数 \(g_{n-1}\)，后者方案数 \(g_{n-3}\)，再乘上此次划分的贡献 \((n-1)^2\)，因此这种情况的答案就是 \((n-1)^2n(g_{n-1}+g_{n-3})\)。
• 如果存在两条及以上长度为 \(n\) 的边，那么我们就枚举 \(1\) 号花朵所在的连续段的长度 \(i\)，不妨设 \(1\) 连了长度为 \(n\) 的边，那么显然它可以旋转一个角度，使得 \(1\) 没有连长度为 \(n\) 的边，并且 \(1\) 所在的连续段长度依然为 \(i\)，这种旋转的方案数为 \(i\)。接下来考虑怎样计算划分的贡献，还是分是否存在特殊图形考虑，如果 \(1,i\) 两边都不存在特殊图形，那么划分的贡献就是 \(g_{i-1}(i-1)^2f_{n-i,0}\)，如果 \(1,i\) 两边都不存在特殊图形，那么划分的贡献是 \(g_{i-3}(i-1)^2f_{n-i,2}\)，如果一边存在一边不存在那么划分的方案数为 \(g_{i-2}(i-1)^2f_{n-i,1}\times 2\)，把三者加起来再乘个 \(i\) 即可，可得总方案数为 \(i(g_{i-1}(i-1)^2f_{n-i,0}+2g_{i-2}(i-1)^2f_{n-i,1}+g_{i-3}(i-1)^2f_{n-i,2})\)

于是这题就做完了，复杂度 \(n\log^2n\)（如果你有耐心手推多项式求逆那应该也能搞到 \(n\log n\)，不过反正我懒癌细胞发作懒得推了），就本题的数据范围，足矣。不过似乎还有神仙给出了线性的做法，这种做法需要用到线性递推的一些 trick，而我还没有深入学习线性递推，就先鸽着罢（（（

这篇题解也是码死我了，题解长度堪比这篇题解

const int pr=3;
const int MAXN=5e4;
const int MAXP=1<<17;
const int MOD=998244353;
const int ipr=(MOD+1)/3;
int qpow(int x,int e=MOD-2){
	int ret=1;
	for(;e;e>>=1,x=1ll*x*x%MOD) if(e&1) ret=1ll*ret*x%MOD;
	return ret;
}
int n,rev[MAXP+5];
int g[MAXN+5],G[MAXN+5][3],dp[MAXN+5][3];
void NTT(vector<int> &a,int len,int type){
	int lg=31-__builtin_clz(len);
	for(int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
	for(int i=0;i<len;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
	for(int i=2;i<=len;i<<=1){
		int W=qpow((type<0)?ipr:pr,(MOD-1)/i);
		for(int j=0;j<len;j+=i){
			int w=1;
			for(int k=0;k<(i>>1);k++,w=1ll*w*W%MOD){
				int X=a[j+k],Y=1ll*w*a[(i>>1)+j+k]%MOD;
				a[j+k]=(X+Y)%MOD;a[(i>>1)+j+k]=(X-Y+MOD)%MOD;
			}
		}
	}
	if(type==-1){
		int ivn=qpow(len);
		for(int i=0;i<len;i++) a[i]=1ll*a[i]*ivn%MOD;
	}
}
vector<int> conv(vector<int> a,vector<int> b){
	int len=1;while(len<a.size()+b.size()) len<<=1;
	a.resize(len,0);b.resize(len,0);NTT(a,len,1);NTT(b,len,1);
	for(int i=0;i<len;i++) a[i]=1ll*a[i]*b[i]%MOD;
	NTT(a,len,-1);return a;
}
void cdq_FFT(int l,int r){
	if(l==r){
		dp[l][0]=(dp[l][0]+G[l][0])%MOD;
		dp[l][1]=(dp[l][1]+G[l][1])%MOD;
		dp[l][2]=(dp[l][2]+G[l][2])%MOD;
		return;
	} int mid=l+r>>1;cdq_FFT(l,mid);
	vector<int> a,b,c;
	for(int i=l;i<=mid;i++) a.pb(dp[i][0]);
	for(int i=0;i<=r-l+1;i++) b.pb(G[i][0]);c=conv(a,b);
	for(int i=mid+1;i<=r;i++) dp[i][0]=(dp[i][0]+c[i-l])%MOD;
	a.clear();b.clear();
	for(int i=l;i<=mid;i++) a.pb(dp[i][1]);
	for(int i=0;i<=r-l+1;i++) b.pb(G[i][1]);c=conv(a,b);
	for(int i=mid+1;i<=r;i++) dp[i][0]=(dp[i][0]+c[i-l])%MOD;
	for(int i=mid+1;i<=r;i++) dp[i][2]=(dp[i][2]+c[i-l])%MOD;
	a.clear();b.clear();
	for(int i=l;i<=mid;i++) a.pb(dp[i][0]);
	for(int i=0;i<=r-l+1;i++) b.pb(G[i][1]);c=conv(a,b);
	for(int i=mid+1;i<=r;i++) dp[i][1]=(dp[i][1]+c[i-l])%MOD;
	a.clear();b.clear();
	for(int i=l;i<=mid;i++) a.pb(dp[i][1]);
	for(int i=0;i<=r-l+1;i++) b.pb(G[i][2]);c=conv(a,b);
	for(int i=mid+1;i<=r;i++) dp[i][1]=(dp[i][1]+c[i-l])%MOD;
	a.clear();b.clear();
	for(int i=l;i<=mid;i++) a.pb(dp[i][2]);
	for(int i=0;i<=r-l+1;i++) b.pb(G[i][2]);c=conv(a,b);
	for(int i=mid+1;i<=r;i++) dp[i][2]=(dp[i][2]+c[i-l])%MOD;
	a.clear();b.clear();
	cdq_FFT(mid+1,r);
}
int main(){
	scanf("%d",&n);g[0]=g[2]=1;
	for(int i=4;i<=n;i+=2) g[i]=(g[i-2]+g[i-4])%MOD;
	for(int i=1;i<=n;i++){
		G[i][0]=1ll*g[i-1]*(i-1)%MOD*(i-1)%MOD;
		G[i][1]=1ll*g[i-2]*(i-1)%MOD*(i-1)%MOD;
		G[i][2]=1ll*g[i-3]*(i-1)%MOD*(i-1)%MOD;
	} cdq_FFT(1,n);int ans=1ll*n*(G[n][0]+G[n][2])%MOD;
	for(int i=2;i<=n-2;i++){
		ans=(ans+1ll*(1ll*G[i][0]*dp[n-i][0]+2ll*G[i][1]*dp[n-i][1]+
		1ll*G[i][2]*dp[n-i][2])%MOD*i%MOD)%MOD;
	} printf("%d\n",ans);
	return 0;
}