Codeforces 1089I - Interval-Free Permutations（析合树计数）

Codeforces 题面传送门 & 洛谷题面传送门

首先题目中涉及排列的 interval，因此可以想到析合树。由于本蒟蒻太菜了以至于没有听过这种神仙黑科技，因此简单介绍一下这种数据结构：我们注意到排列的区间有一个性质：对于排列中的两段区间 \(X,Y\)，如果它们有交，那么必然有 \(X\cap Y,X\cup Y,X\setminus(X\cap Y),Y\setminus(X\cap Y)\) 四个集合均为区间，也就是说连续段之间只有包含没有相交关系，因此它们可以表示为一棵树形结构。

我们考虑用一棵根节点为区间 \([1,n]\)，叶子节点为每个长度为 \(1\) 的区间的树表示这个树形结构，对于每个区间我们定义它的本原连续段为极大的、彼此之间不存在部分相交的连续段，举个例子，排列 \([5,1,4,2,3]\) 有两个本原连续段：\([5],[1,4,2,3]\)——显然我们能够找到这样的连续段组成的集合。那么我们就令这个区间的儿子为这些本原连续段们，继续递归下去即可建出这棵树。由于这棵树的叶子节点恰有 \(n\) 个，因此这棵树的节点数也是线性的。

考虑将这棵树的节点分分类，由于每个节点的儿子们都是一个个区间，因此我们可以将它们离散化成一个个在 \([1,\text{儿子个数}]\) 之内的数，我们称这样得到的排列为儿子排列，手玩几组数据即可发现对于每个点而言，它的儿子排列总共只有两种类型，否则就不满足“本原连续段”的定义了：

• 儿子排列从左到右恰好为 \(1,2,3,\cdots,\text{儿子个数}\) 或者 \(\text{儿子个数},\cdots,3,2,1\)，我们称这样的点为合点
• 儿子排列中除了整个区间和长度为 \(1\) 的子区间不存在任何其他连续段，我们称这样的点为析点

比方说排列 \([9,1,10,3,2,5,7,6,8,4]\) 建出树来如下图所示：

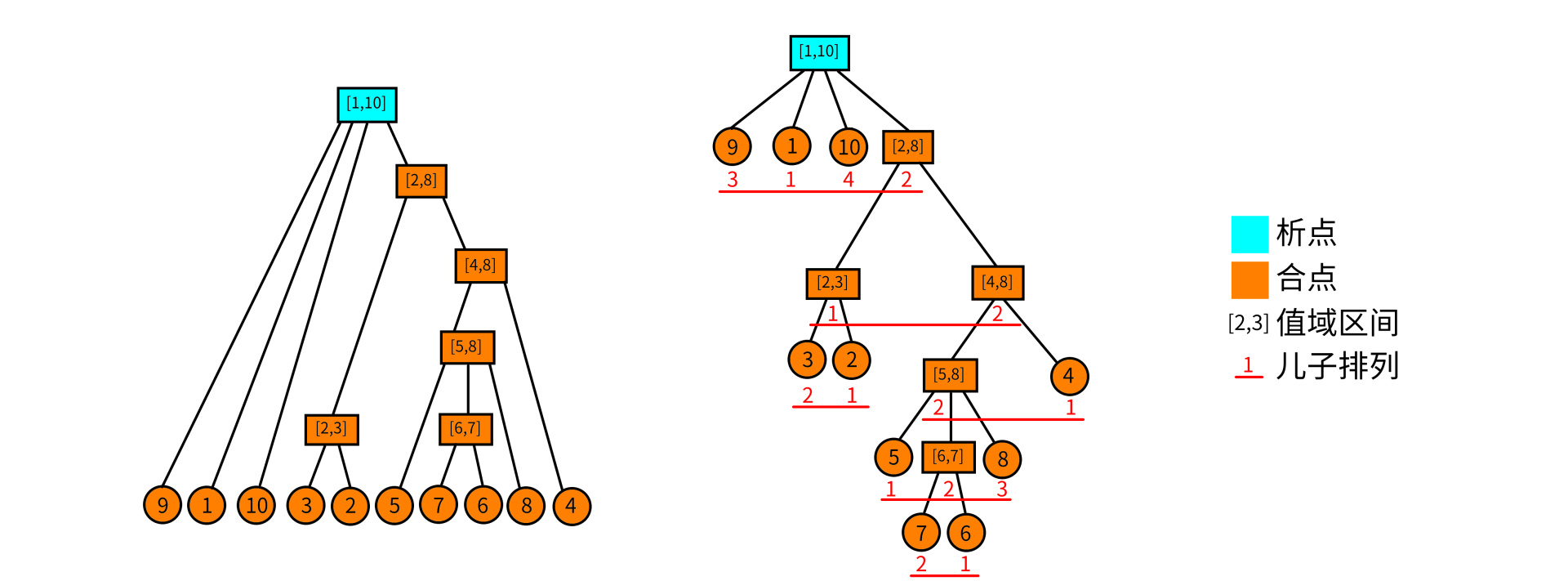
析合树有以下性质：

• 每个析点儿子个数一定 \(\ge 4\)，因为任何长度为 \(3\) 的排列都存在非平凡连续段
• 如果我们指定一棵树上每个节点的析合性，并满足析点儿子个数 \(\ge 4\)，合点儿子个数 \(\ge 2\)，那么一定存在某个排列对应这棵树

回到此题来，此题等价于求儿子个数为 \(n\)，且根为析点的排列个数 \(f_n\)，直接求不太容易，因此考虑正难则反，那总排列数减去不合法的排列个数，前者就是 \(n!\)，后者可以分情况讨论：

1. 根是析点，那么我们可以枚举根节点的儿子个数 \(c\ge 4\)，那么我们要将 \(n\) 个节点划分成 \(c\) 个区间，每个区间内的元素随便乱排，最后还要将这 \(c\) 个区间排成一列满足不存在非平凡区间，很显然我们可以将这个任务分成两部分，划分儿子和确定儿子排列，后者方案数显然就是 \(f_c\)，前者可以设一个 \(s_{i,j}\) 表示将 \(i\) 个节点划分成 \(j\) 段的方案数，显然有 \(s_{i,j}=\sum\limits_{k<i}s_{i-k,j-1}·k!\)
2. 根是合点，那么我们不妨假设根节点的儿子排列为 \(1,2,3,\cdots\)，对于单调递减的情况乘个 \(2\) 即可，根据合点的定义必然存在某个前缀 \(i\) 满足 \(p[1...i]\) 恰好为 \([1,i]\) 的排列，我们就考虑枚举这个最小的 \(i\)，记 \(g_i\) 为长度为 \(i\) 的、且存在某个长度不等于 \(i\) 的前缀 \(p[1...j]\) 为 \([1,j]\) 的排列的排列 \(p\) 的个数，那么有 \(g_i=i!-\sum\limits_{j<i}g_j(i-j)!\)，根是合点的总数也就自然是 \(2g_n\)。

简单递推一下即可，复杂度三方。

const int MAXN=400;
int mod,fac[MAXN+5],ifac[MAXN+5],dp[MAXN+5],s[MAXN+5][MAXN+5],f[MAXN+5];
void init(int n){
	for(int i=(fac[0]=ifac[0]=ifac[1]+1);i<=n;i++) ifac[i]=1ll*ifac[mod%i]*(mod-mod/i)%mod;
	for(int i=1;i<=n;i++) fac[i]=1ll*fac[i-1]*i%mod,ifac[i]=1ll*ifac[i-1]*ifac[i]%mod;
	f[1]=1;
	for(int i=2;i<=n;i++){
		for(int j=1;j<i;j++) f[i]=(f[i]+1ll*f[j]*fac[i-j])%mod;
		f[i]=(fac[i]-f[i]+mod)%mod;
	} s[0][0]=1;
	for(int i=1;i<=n;i++) for(int j=1;j<=i;j++) for(int k=1;k<=i;k++)
		s[i][j]=(s[i][j]+1ll*s[i-k][j-1]*fac[k])%mod;
	dp[2]=(dp[1]=(dp[3]=0)+1)+1;
	for(int i=4;i<=n;i++){
		int sum1=0,sum2=0;
		for(int j=1;j<i;j++) sum1=(sum1+1ll*f[j]*fac[i-j])%mod;
		for(int j=4;j<i;j++) sum2=(sum2+1ll*dp[j]*s[i][j])%mod;
		int sub=(2ll*sum1+sum2)%mod;dp[i]=(fac[i]-sub+mod)%mod;
	}
}
int main(){
	int qu;scanf("%d%d",&qu,&mod);init(MAXN);
	while(qu--){
		int n;scanf("%d",&n);
		printf("%d\n",dp[n]);
	}
	return 0;
}