存储系统的基本数据结构之一: 跳表 (SkipList)

在接下来的系列文章中，我们将介绍一系列应用于存储以及IO子系统的数据结构。这些数据结构相互关联又有着巨大的区别，希望我们能够不辱使命的将他们分门别类的介绍清楚。本文为第一节，介绍一个简单而又有用的数据结构：跳表 (SkipList)

---

在对跳表进行讨论之前，我们首先描述一下跳表的核心思想。

跳表(Skip List)是有序线性链表的一种。通常对线性链表进行查找需要遍历，因而不能很好的使用二分查找这样快速的方法（想像一下在链表中定位中间元素的复杂度）。为了提高查找速率，我们可以将这些线性链表打散，组织成树结构，这样的树就叫做查找树。查找树中尤以平衡查找树的查找代价最小，因此平衡二叉查找树成为了在内存中进行查找的最佳的数据结构。红黑树作为平衡二叉查找树的一种实现，经常被我们用在这种场景之中。

然而，平衡树就一定需要平衡化。在对树进行一系列的插入删除之后，树不再平衡了，此时就需要调整平衡的算法。红黑树的复杂性就体现在这里，相信所有写过红黑树的童鞋都记忆犹新。

就在此时，晴天一个霹雳，跳表诞生了[1]。它支持快速检索且不需要复杂的平衡操作，由于它的简单性，使得它往往比红黑树还有更好的性能表现。

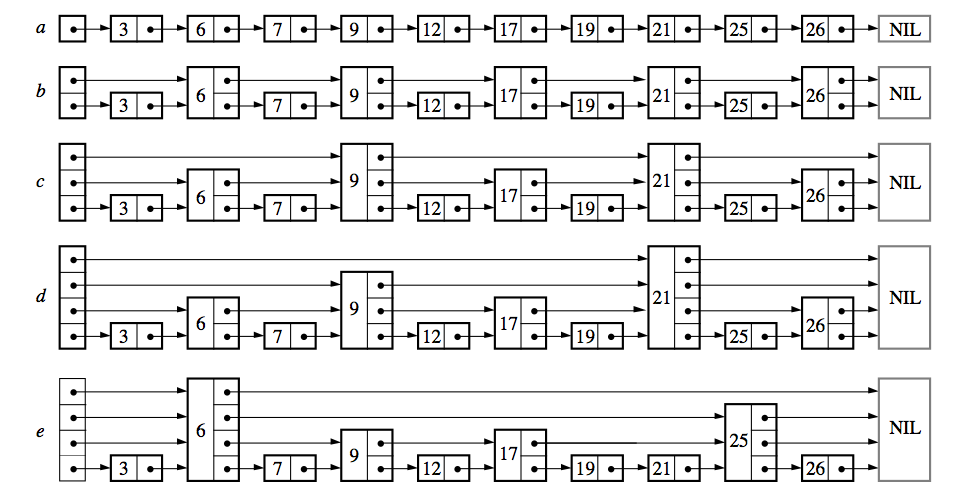
上图就是一个跳表的示意图，图中 (a) 是一个正常的有序列表，而 (b) 到 (e) 则是不同level的跳表。

定义：

对于一个节点，如果它有k个指针，那么就称之为一个 level k 节点。

一个跳表的最大 level 是当前在列表中最大的节点的 level。对于空列表, level为1.

推论：

如果每第 (2ⁱ) 个节点有一个指针指向向后数 (2ⁱ) 节点，而不是指向紧接着的那个节点，那么所有的节点基本上会满足这样一个分布：50%的节点位于level 1，25%的节点位于level 2，12.5%的节点位于level 3 等等。

如果某个节点的level是随机选择的，且随机所遵守的分布符合上个推论所描述，那么 level k 节点的第 i 个指针只需要指向下一个 level 大于等于 i 的节点就构造如上图所示的跳表，并不需要一定要严格指向第 i^i-1 个节点。

算法：

1> 初始化

只创建第一个列表，该列表的leve值就是1。

2> 检索

a) 搜索从最大level的列表开始，找到比要检索的key小的最大的那个元素

b) 如果不能找到，减少一个level继续检索

c) 如果在level 1一层也不能找到，那就说明所要找的元素一定在当前停下的位置的下一个节点

Search(list, key)
{
    x = list->header
    for (i = list.level; i >= 1; i--)
    {
        while (x->forward[i]->key < key)
           x = x->forward[i]
    }
    x = x->forward[1]
   if (x->key == key) return x->vlaue
   else return failure
}

3> 插入

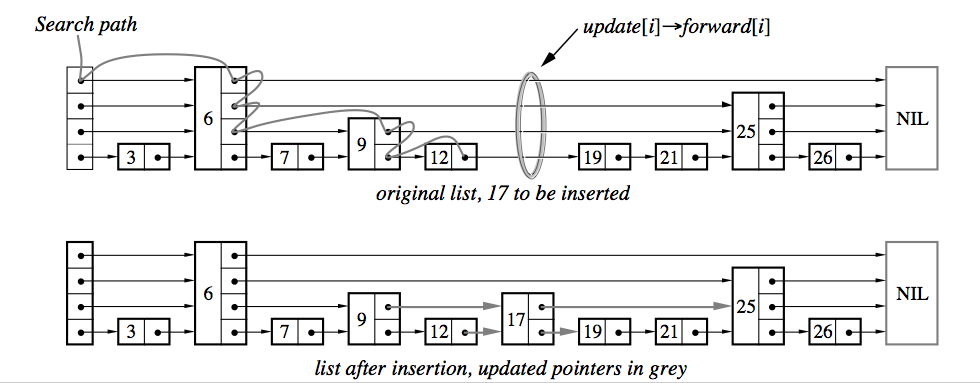
a) 检索要插入的key是否存在，如果存在那么更新value即可

b) 如果不存在，则需要插入。需要注意的是，在检索的过程中，我们应当用一个数组 update[1...MaxLevel] 来保存每一个 level 中搜索停止的节点，这些节点用于后来指向新加入的节点

c) 产生一个新节点，随机的给定该节点的level。如果随机出来的level比当前最大的level还要大，那么扩大 update 数组到新的 MaxLevel 个元素，并且将新增的 update 元素设置为 list 的 header

d) 从 1 开始到 MaxLevel，将新节点的 forward 数据设置为 update[i...MaxLevel] 的值；而将 update[i...MaxLevel] 的 forward[i] 设置为 x.

 insert(list, key, value){
   local update[...MaxLevel]
   x = list->header
   for i = list->level downto  do
     while x->forward[i]->key < key
       x = x->forward[i]
    update[i] = x
   if x->key == key then x->value = value;
   else
     lvl = randomLevel()
     if lvl > list->level then
       for i = list->level +  to lvl
         update[i] = list->header
       list->level = lvl
     x = MakeNode(lvl, key, value)
     for i =  to level
      x->forward[i] = update[i]->forward[i];
      update[i]->forward[i] = x;
 } 

> 选择新节点的level

新节点的level完全由一个随机函数产生：

 randomLevel()
     lvl =
     while random() < p and lvl < MaxLevel do
       lvl = lvl +
     return lvl

复杂度分析：

搜索复杂度的分析方法很简单，结论是非常确定的O(logn)，那剩下的比较就是常数项了，如下图所示：

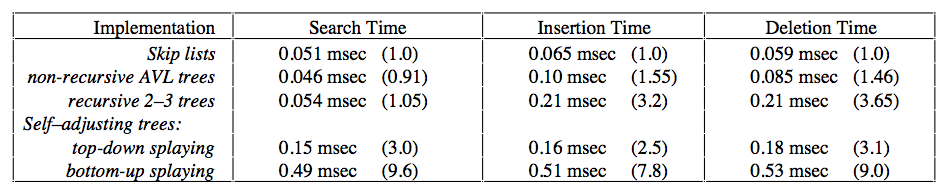
可以看出来，跳表还是有很大的常数项优势的。

－－ Reference －－

[1] William Pugh, 1990, Communications of the ACM 33.6, Skip Lists: A Probabilistic Alternative to Balanced Trees.