dp--2019南昌网络赛B-Match Stick Game

dp--2019南昌网络赛B-Match Stick Game

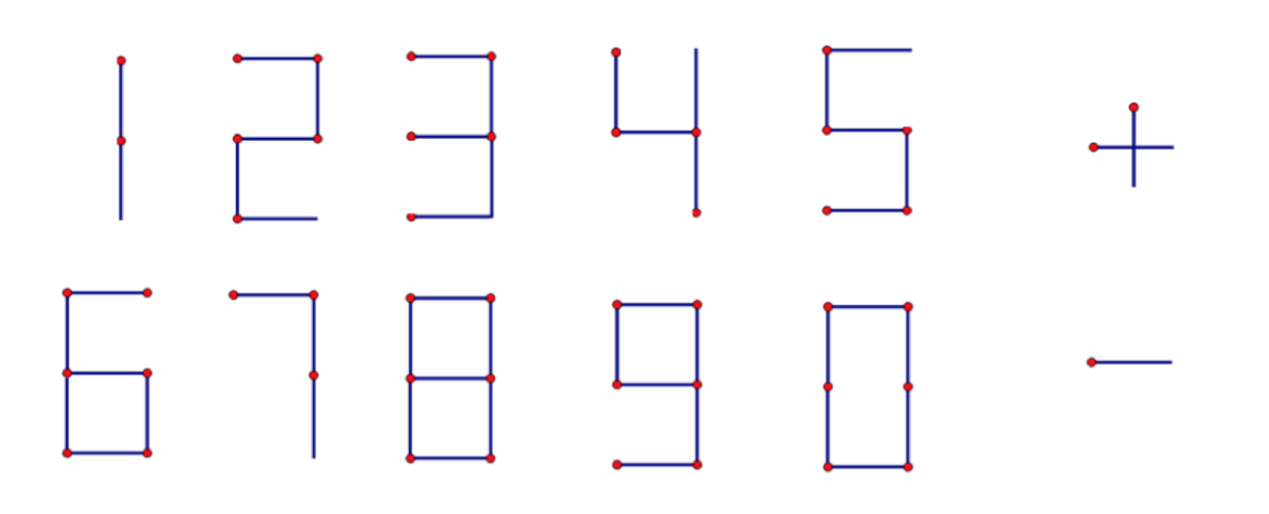
Xiao Ming recently indulges in match stick game and he thinks he is good at it. His friend Xiao Jun decides to test him. Xiao Jun gives him an expression of length , made by match sticks and asks him to calculate the maximum value of the expression by moving any match sticks (but he can’t discard any of them). The expression is made up of some numbers, plus signs and minus signs represented as A_1 \ op_1 \ A_2 \ op_2 \ A_3 \ op_3 \ \cdots A_{m - 1} \ op_{m - 1} \ A_mA1 o**p1 A2 o**p2 A3 o**p3 ⋯A**m−1 opm−1 A**m. mm must be count by himself, A_k(1 \le k \le m)A**k(1≤k≤m) is an integer without leading zeros and less than 10^9109 , op_k (1 \le k \le m)opk(1≤k≤m) is a plus sign or a minus sign. At the same time, there are some requirements of the new expression:

1. The new expression should also be made up of mm numbers and m - 1m−1 operators.
2. The number of digits per number should keep consistent with the original.
3. There couldn’t be any leading zeros per number.

Input

The first line consists of a single integer TT denoting the number of test cases.

There’re two lines in each test case.

The first line contains an integer nn.

A string of length nn follows in the next line, denoting the expression given.

The expression is guaranteed to be valid.

Output

For each test case, print a single integer denoting the maximum result of the expression.

Constraints

\[1≤n≤100
\]

Note

Expression with the maximum result for the second sample is 7 - 17−1 .

Expression with the maximum result for the second sample is 7 + 7 + 97+7+9.

样例输入复制

3
3
1-1
3
1+1
5
1+2+3

样例输出复制

0
6
23

题意

给你一条式子，式子有火柴棒组成，可以移动火柴棒，要求：式子中运算符号的数目不变，即进行运算的数字数量不变。每组进行运算的数的位数不变。火柴棒的数目不变。式子最后得到的结果最大。

思路

把式子看成多组数进行加减运算

预处理:mx[i][j]表示在一组数中，第i位用了j根火柴所能达到的最大值，mi[i][j]同理为最小值

考虑加减号，状态转移看代码，dp[i][j]表示这条式子中用i组数，j根火柴所能达到的最大值

#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <cmath>
#include <sstream>
#include <algorithm>
#include <set>
#include <map>
#include <vector>
#include <queue>
#include <iomanip>
#include <stack>

using namespace std;

typedef long long LL;
const int INF = 0x3f3f3f3f;
const int N = 1e7 + 50;
const int MOD = 1e9 + 9;

#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
#define F(i, l, r) for(int i = l;i <= (r);++i)
#define RF(i, l, r) for(int i = l;i >= (r);--i)

int p[] = {6, 2, 5, 5, 4, 5, 6, 3, 7, 6};//0123456789
int sum, num, n;
string s;
LL dp[105][1005], dig[105];//第i组数第用j根火柴能到的最大值，每组数的位数
LL mx[15][1005], mi[15][1005];//一组数中第i位用j火柴可以到的最值

void solve()
{
    fill(mx[0], mx[0] + 15 * 1005, -1);
    fill(mi[0], mi[0] + 15 * 1005, INF);
    mx[0][0] = mi[0][0] = 0;
    F(i, 1, 11)//根据题目，最多有9位数
        F(j, 0, i * 7)//一个数字最多用7根火柴
            F(k, 0, 9)
            {
                if(p[k] > j) continue;
                mx[i][j] = max(mx[i][j], mx[i - 1][j - p[k]] * 10 + k);
                mi[i][j] = min(mi[i][j], mi[i - 1][j - p[k]] * 10 + k);
            }

    memset(dp, -1, sizeof(dp));
    memset(dig, 0, sizeof(dig));
    int len = s.size();
    sum = 0, num = 1;//火柴数，组数
    F(i, 0, len - 1)
    {
        if(s[i] == '+') {num++; sum += 2;}
        else if(s[i] == '-') {num++; sum++;}
        else {sum += p[s[i] - '0']; dig[num]++;}
    }
    F(i, 1, sum)
        dp[1][i] = mx[dig[1]][i];
    F(i, 2, num)//num组数
        F(j, 0, sum)//一共的火柴数
            F(k, 1, 7 * dig[i])//该组数所用的火柴数
            {
                if(j >= 2 + k && dp[i - 1][j - 2 - k] != -1 && mx[dig[i]][k] != -1)//火柴数目够，且前一组数有答案，且这一组数用k根火柴有最值
                    dp[i][j] = max(dp[i][j], dp[i - 1][j - 2 - k] + mx[dig[i]][k]);
                if(j >= 1 + k && dp[i - 1][j - 1 - k] != -1 && mi[dig[i]][k] != INF)
                    dp[i][j] = max(dp[i][j], dp[i - 1][j - 1 - k] - mi[dig[i]][k]);
            }
}

int main()
{
    int T;
    cin >> T;
    while(T--)
    {
        cin >> n >> s;
        solve();
        cout << dp[num][sum] << endl;
    }
    return 0;
}

参考博客