CodeForces - 459E Pashmak and Graph[贪心优化dp]

E. Pashmak and Graph

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Pashmak's homework is a problem about graphs. Although he always tries to do his homework completely, he can't solve this problem. As you know, he's really weak at graph theory; so try to help him in solving the problem.

You are given a weighted directed graph with n vertices and m edges. You need to find a path (perhaps, non-simple) with maximum number of edges, such that the weights of the edges increase along the path. In other words, each edge of the path must have strictly greater weight than the previous edge in the path.

Help Pashmak, print the number of edges in the required path.

Input

The first line contains two integers n, m (2 ≤ n ≤ 3·105; 1 ≤ m ≤ min(n·(n - 1), 3·105)). Then, m lines follows. The i-th line contains three space separated integers: ui, vi, wi (1 ≤ ui, vi ≤ n; 1 ≤ wi ≤ 105) which indicates that there's a directed edge with weight wi from vertex ui to vertex vi.

It's guaranteed that the graph doesn't contain self-loops and multiple edges.

Output

Print a single integer — the answer to the problem.

Examples

input

3 3
1 2 1
2 3 1
3 1 1

output

1

input

3 3
1 2 1
2 3 2
3 1 3

output

3

input

6 7
1 2 1
3 2 5
2 4 2
2 5 2
2 6 9
5 4 3
4 3 4

output

6

Note

In the first sample the maximum trail can be any of this trails: .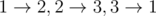

In the second sample the maximum trail is .

In the third sample the maximum trail is .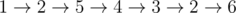

/*
显而易见的贪心——小的边排前面……所以，先按照边长排序，然后dp，以当前边的尾节点为路径的结尾，然后一个边的首段点为u，尾端点为v,
裸地转移就是dp[v]=max(dp[v],dp[u]+1)
注意边相等要单独处理，然后就AC了……
*/
#include<cstdio>
#include<algorithm>
#include<iostream>
using namespace std;
const int N=3e5+;
struct edge{int x,y,z;}e[N<<];
int n,m;int f[N],g[N];
bool operator <(const edge &a,const edge &b){
    return a.z<b.z;
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=;i<=m;i++) scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].z);
    sort(e+,e+m+);
    for(int j,i=;i<=m;i++){
        for(j=i;e[j].z==e[i].z;j++) g[e[j].y]=max(g[e[j].y],f[e[j].x]+);
        for(j=i;e[j].z==e[i].z;j++) f[e[j].y]=g[e[j].y];
        i=j-;
    }
    printf("%d\n",*max_element(f+,f+n+));
    return ;
}