JS实现图的创建和遍历
图分为无向图和有向图
图的存储结构有邻接矩阵、邻接表、十字链表、邻接多重表这四种,最常用的是前两种
本篇主要是利用邻接矩阵实现无向图的创建和遍历(深度优先、广度优先),深度优先其实就是二叉树里的前序遍历


利用邻接矩阵(边数组)创建图
let scanf = require('scanf');
//定义邻接矩阵
let Arr2 = [
[0, 1, 0, 0, 0, 1, 0, 0, 0],
[1, 0, 1, 0, 0, 0, 1, 0, 1],
[0, 1, 0, 1, 0, 0, 0, 0, 1],
[0, 0, 1, 0, 1, 0, 1, 1, 1],
[0, 0, 0, 1, 0, 1, 0, 1, 0],
[1, 0, 0, 0, 0, 0, 1, 0, 0],
[0, 1, 0, 1, 0, 1, 0, 1, 0],
[0, 0, 0, 1, 1, 0, 1, 0, 0],
[0, 1, 1, 1, 0, 0, 0, 0, 0],
]
let numVertexes = 9, //定义顶点数
numEdges = 14; //定义边数
// 定义图结构
function MGraph() {
this.vexs = []; //顶点表
this.arc = []; // 邻接矩阵,可看作边表
this.numVertexes = null; //图中当前的顶点数
this.numEdges = null; //图中当前的边数
}
let G = new MGraph(); //创建图使用
//创建图
function createMGraph() {
G.numVertexes = numVertexes; //设置顶点数
G.numEdges = numEdges; //设置边数
//录入顶点信息
for (let i = 0; i < G.numVertexes; i++) {
G.vexs[i] = scanf('%s'); //String.fromCharCode(i + 65); ascii码转字符
}
console.log(G.vexs) //打印顶点
//邻接矩阵初始化
for (let i = 0; i < G.numVertexes; i++) {
G.arc[i] = [];
for (j = 0; j < G.numVertexes; j++) {
G.arc[i][j] = Arr2[i][j]; //INFINITY;
}
}
/**以下是手动录入的方式 */
// for (let k = 0; k < G.numEdges; k++) {
// console.log('输入边(vi,vj)上的下标i,下标j和权w:');
// let rlt = scanf('%d,%d,%d');
// let i = rlt[0], j = rlt[1], w = rlt[2];
// G.arc[i][j] = w;
// G.arc[j][i] = G.arc[i][j]; //无向图,矩阵对称
// }
console.log(G.arc); //打印邻接矩阵
}
深度优先遍历
let visited = []; //访问标志数组,遍历时使用 //邻接矩阵的深度优先递归算法
function DFS(i) {
visited[i] = true;
console.log('打印顶点:', G.vexs[i]) //打印顶点 ,也可以其他操作
for (let j = 0; j < G.numVertexes; j++) {
if (G.arc[i][j] == 1 && !visited[j]) {
console.log(G.vexs[i], '->', G.vexs[j])
DFS(j) //对未访问的顶点进行递归
}
}
}
//邻接矩阵的深度遍历操作
function DFSTraverse() {
for (let i = 0; i < G.numVertexes; i++) {
visited[i] = false;
}
for (let i = 0; i < G.numVertexes; i++) {
if (!visited[i])
DFS(i)
}
}
广度优先遍历
//邻接矩阵的广度遍历算法
function BFSTraverse() {
let queue = []; //初始化队列
for (let i = 0; i < G.numVertexes; i++) {
visited[i] = false;
}
for (let i = 0; i < G.numVertexes; i++) { //对每一个顶点做循环
if (!visited[i]) { //如果没有访问过就处理
visited[i] = true;
console.log('打印顶点:', G.vexs[i]) //也可以是其他操作
queue.push(i); //将此顶点入队列
while (queue.length != 0) { //当前队列不为空
queue.shift();
for (let j = 0; j < G.numVertexes; j++) {
//判断其他顶点若与当前顶点存在边且未访问过
if (G.arc[i][j] == 1 && !visited[j]) {
visited[j] = true;
console.log(G.vexs[i], '->', G.vexs[j])
console.log('打印顶点:', G.vexs[j])
queue.push(j) //将此顶点放入队列
}
}
}
}
}
}
运行:
结果:
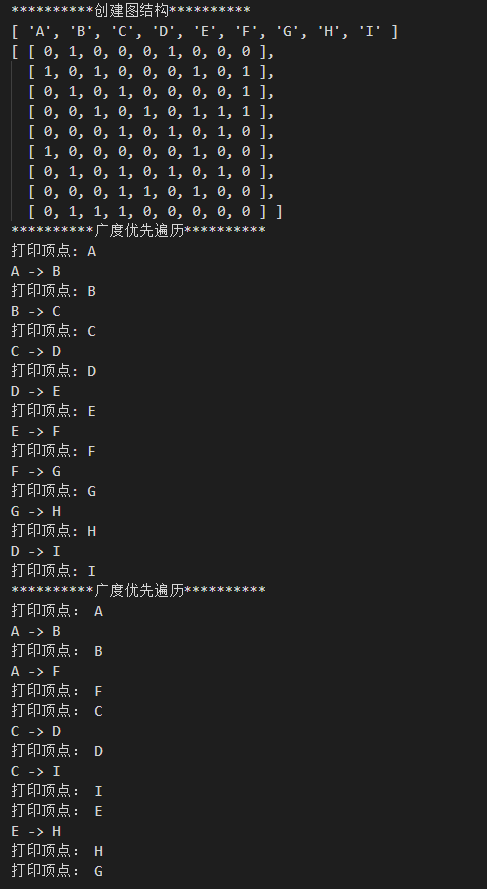
JS实现图的创建和遍历的更多相关文章
- 图的创建和遍历(BFS/DFS)
图的表示方法主要有邻接矩阵和邻接表.其中邻接表最为常用,因此这里便以邻接表为例介绍一下图的创建及遍历方法. 创建图用到的结构有两种:顶点及弧 struct ArcNode { int vertexIn ...
- JS DOM操作(创建、遍历、获取、操作、删除节点)
创建节点 <!DOCTYPE html> <html lang="zh-CN"> <head> <meta charset="u ...
- JS实现二叉树的创建和遍历
1.先说二叉树的遍历,遍历方式: 前序遍历:先遍历根结点,然后左子树,再右子树 中序遍历:先遍历左子树,然后根结点,再右子树 后续遍历:先遍历左子树,然后右子树,再根结点 上代码:主要还是利用递归 ...
- 数据结构代码整理(线性表,栈,队列,串,二叉树,图的建立和遍历stl,最小生成树prim算法)。。持续更新中。。。
//归并排序递归方法实现 #include <iostream> #include <cstdio> using namespace std; #define maxn 100 ...
- 【算法导论】图的深度优先搜索遍历(DFS)
关于图的存储在上一篇文章中已经讲述,在这里不在赘述.下面我们介绍图的深度优先搜索遍历(DFS). 深度优先搜索遍历实在访问了顶点vi后,访问vi的一个邻接点vj:访问vj之后,又访问vj的一个邻接点, ...
- 【算法导论】图的广度优先搜索遍历(BFS)
图的存储方法:邻接矩阵.邻接表 例如:有一个图如下所示(该图也作为程序的实例): 则上图用邻接矩阵可以表示为: 用邻接表可以表示如下: 邻接矩阵可以很容易的用二维数组表示,下面主要看看怎样构成邻接表: ...
- JS前端图形化插件之利器Gojs组件(php中文网)
JS前端图形化插件之利器Gojs组件(php中文网) 一.总结 一句话总结:php中文网我可以好好走一波 二.JS前端图形化插件之利器Gojs组件 参考: JS前端图形化插件之利器Gojs组件-js教 ...
- JS对象—数组总结(创建、属性、方法)
JS对象—数组总结(创建.属性.方法) 1.创建字符串 1.1 new Array() var arr1 = new Array(); var arr2 = new Array(6); 数组的长度为6 ...
- js正则表达式图形化工具-rline
github地址:https://github.com/finance-sh/rline 在线demo: http://lihuazhai.com/demo/test.html 这是一个js正则表达式 ...
随机推荐
- [bzoj4712]洪水 线段树+树链剖分维护动态dp+二分
Description 小A走到一个山脚下,准备给自己造一个小屋.这时候,小A的朋友(op,又叫管理员)打开了创造模式,然后飞到山顶放了格水.于是小A面前出现了一个瀑布.作为平民的小A只好老实巴交地爬 ...
- 2018 ACM-ICPC 亚洲区域赛北京现场赛 I题 Palindromes
做法:打表找规律 大数是过不了这个题的(但可以用来打表) 先找k的前缀,前缀对应边缘数字是哪个 如果第0位是2-9 对应奇数长度的1-8 第0位为1时,第1位为0时对应奇数长度的9,为1-9时对应偶数 ...
- C#-MVC-强数据类型、TempData、多表单、ajax
一.强数据类型 将某一个或一组数据在控制器传递到视图上去 一个视图里只能有一个强类型数据 强类型数据 - 将某一个或一组数据在控制器传递到视图上去,同ViewBag,数据更稳定,防止多数据传递中出现错 ...
- 采用prometheus 监控mysql
1. prometheus 是什么 开源的系统监控和报警工具,监控项目的流量.内存量.负载量等实时数据. 它通过直接或短时jobs中介收集监控数据,在本地存储所有收集到的数据,并且通过定义好的rule ...
- json兼容ie8
今天遇到一个问题,后台传递过来的json对象,在前端解析的时候用JSON.parse(result)方法不好使,查了一下是因为ie浏览器的问题.然后在网上翻了翻,找到了这个办法,可以使这个函数在ie中 ...
- 响应式Web设计-一种优雅的掌上展现
入门 flat - style (too many ad.) writeshell
- Bomb(要49)--数位dp
Bomb Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/65536 K (Java/Others)Total Submi ...
- 从源码层面解析SpringIOC容器
Spring IOC容器继承关系图 MessageSource支持消息国际化.ResouceLoader资源加载.BeanFactory创建Bean.ApplicationEventPublisher ...
- 查看APK包签名的方法。
1.查看 keystore $ keytool -list -keystore debug.keystore 结果: Keystore type: JKS Keystore provider: SUN ...
- phpspreadsheet开发手记
坑安装简单示例通过模板来生成文件释放内存单元格根据索引获取英文列设置值合并单元格居中显示宽度设置批量设置单元格格式直接输出下载自动计算列宽函数formula单元格变可点击的超链 PhpSpreadsh ...
