支持向量机SVM进阶

本文适合于对SVM基本概念有一点了解的童鞋。

SVM基本概念：

• 最大边缘平面——基本原理：结构风险最小化
• 分类器的泛化误差
• 支持向量

问题描述：

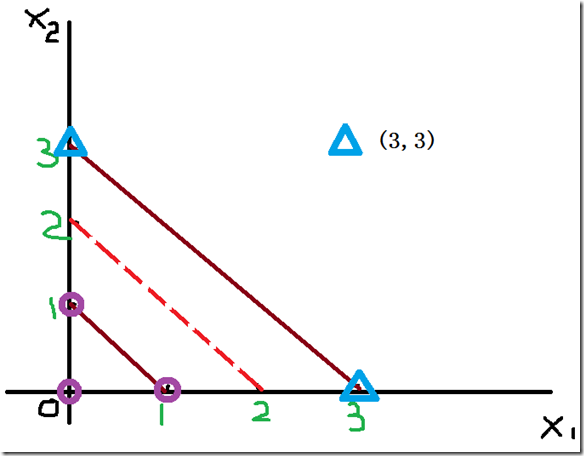
请对一下数据，利用svm对其进行分类。

      最终任务：

           找到最优超平面

  图1

看到这张图之后，发现这是一个线性可分的二分类问题。

数据是这样的：     

	y=1	类别1		y=-1	类别2
	x1	x2		x1	x2
x1	0	0	x4	3	3
x2	1	0	x5	3	0
x3	0	1	x6	0	3

 

好，老师的题目已经出完了，在动手解题之前，我们首先通过观察，可以轻易的发现，最佳的分类超平面就是：x1+x2-2=0

而类别1的支持向量为：x1+x2-1=0

类别2的支持向量为：x1+x2-3=0

好，这个观察的结果可以便于我们稍后通过计算而得出的结果进行一个验算。

 

 

————————————美丽的分割线之STEP1——————————————

下面开始正式的解题环节：

STEP    1，我们可以把这个超平面写成w·x+b=0(w₁x₁+x₂x₂+b=0)的形式（直线表示方法中的一般式），其中w和x都代表向量，w的方向垂直于决策边界。

问题的最终目标就是要得到W和b的值。

如图2：

 

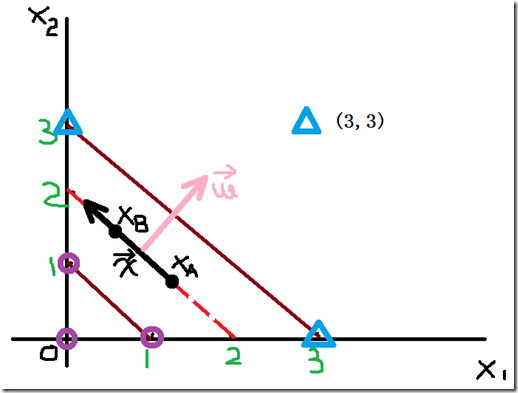
图2

可以看到，点XA(X_A1,X_A2)和点XB(X_B1,X_B2)在决策边界上，因此，他们符合:

w·x_A+b=0

w·x_B+b=0

对于任何在决策边界上方的三角形X_三角形，我们可以证明：

w·x_三角形+b=k    == >    k>0

同理，对于任何在决策边界下方的三角形X_圆形，我们可以证明：

w·x_圆形+b=k’   == >    k’<0

因此，我们可以用以下方式预测任何测试样本z的类型：

类别1    y=1    如果w·z+b>0

类别2    y=-1   如果w·z+b<0

————————————美丽的分割线之STEP2——————————————

下面，我们来考虑一下支持向量，两个超平面可以表示如下：

b_i1:w·x+b=1

b_i2:w·x+b=-1

(PS:这里是一定能够表示为上面的形式，因为你可以对式子两边同时进行等倍的放大和缩小)

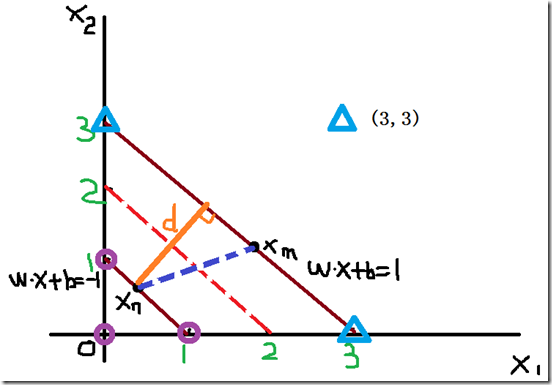
假设，xm和xn分别为类1和类2上的点，那么：

                                                 图3（图画的不太好，请谅解）

将x_m和x_n分别代入公式，则边缘d可以通过两式相减得到：

w·(x1-x2)=2                                     模模cosθ

||w||✕d=2                                       可以理解为点到直线的距离

∴d=2 / ||w||

其中，||w||表示范数，这里的||w||可以理解为向量w的模（向量范数：向量x的2范数是x中各个元素平方之和再开根号），若向量w=(w₁,w₂)，那么||w||=(w₁²+w₂²)^1/2。这里，我们暂时还不知道哪些点是支持向量上的点。

————————————美丽的分割线之STEP3—————————————

SVM的训练目标就是训练出最优的W和b

让我们再来简单回顾一下：

y_i=1:    w·x_i+b≥1

y_i=-1:   w·x_i+b≤-1

这个条件要求，所有类别为1的训练实例(即三角形)，都必须位于超平面w·x+b=1上或位于它的上方，而那些类别为2的训练实例(即圆圈)都必须位于超平面w·x+b=-1上或位于它的下方。我们可以整理出一个比较紧凑的形式：

y_i(w·x_i+b)≥1 , i=1,2(本例中，是二维的，故i取1和2)

尽管前面的条件可以用于其他的线性分类器，但是SVM增加了一个要求：决策边界的边缘必须是最大的。然而，最大化边缘等价于最小化下面的目标函数：

max (d=2 / ||w||)     ==     min (||w||² / 2)

也就是说，我们当前的目的就是

由于目标函数是二次的，而约束在参数w和b上是线性的，因此，这个问题是一个凸(convex)优化问题，可以通过标准的拉格朗日乘子法解决。

整理一下得到该优化问题的拉格朗日算子：

下面，根据题目，我们把具体的数据代入式子展开后得到：

因为拉格朗日乘子是未知的，因此我们仍然不能得到向量w和b的解。请仔细揣摩书上的话：

决策边界的参数w和b仅依赖于这些支持向量

也就是说，我们利用二次规划的方法可以求出在支持向量上的点的λ值（不在支持向量上的点，λ值都为0，即拉格朗日乘子都为0）。

当我们知道所有λ的值之后，根据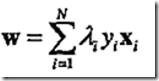我们就可以算出w1和w2，然后在根据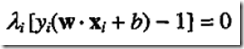就可以求出b的值。

这样，我们就圆满的完成了任务。

————————————美丽的分割线之STEP4——————————————

那么，当线性不可分的时候，我们该如何转化呢？这时就要涉及到一些更高级的东东，未完待续。