MACD背离：

价格创新高而指标却下跌
价格创新低而指标却上涨

缠中说禅背离

多次缠绕中唇吻的面积更小

看图说话：









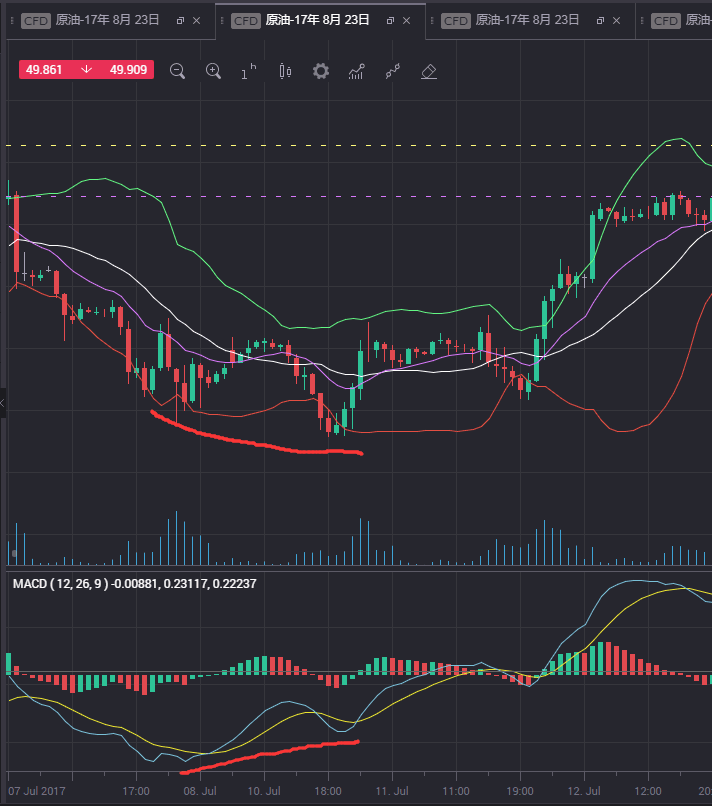
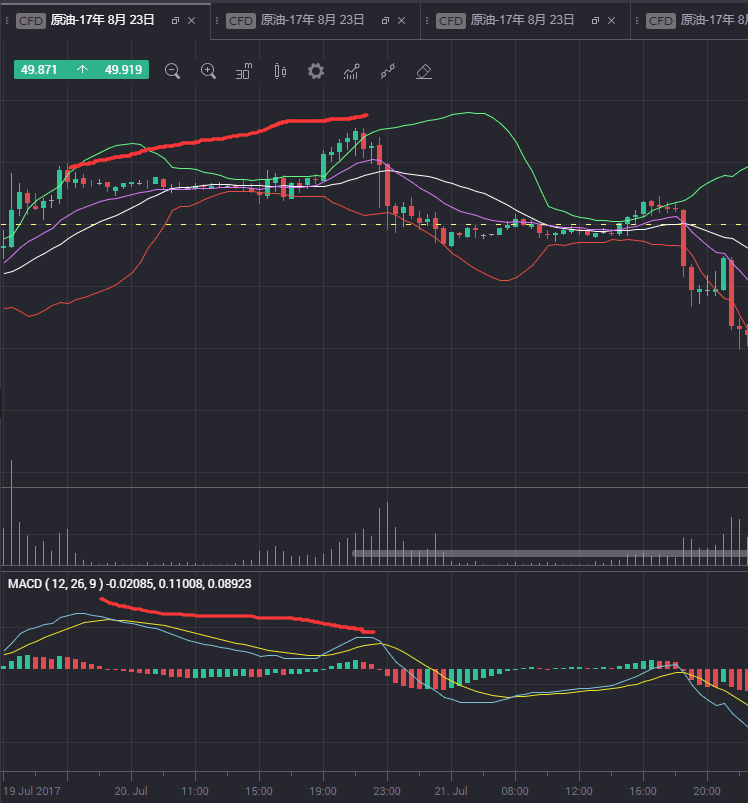
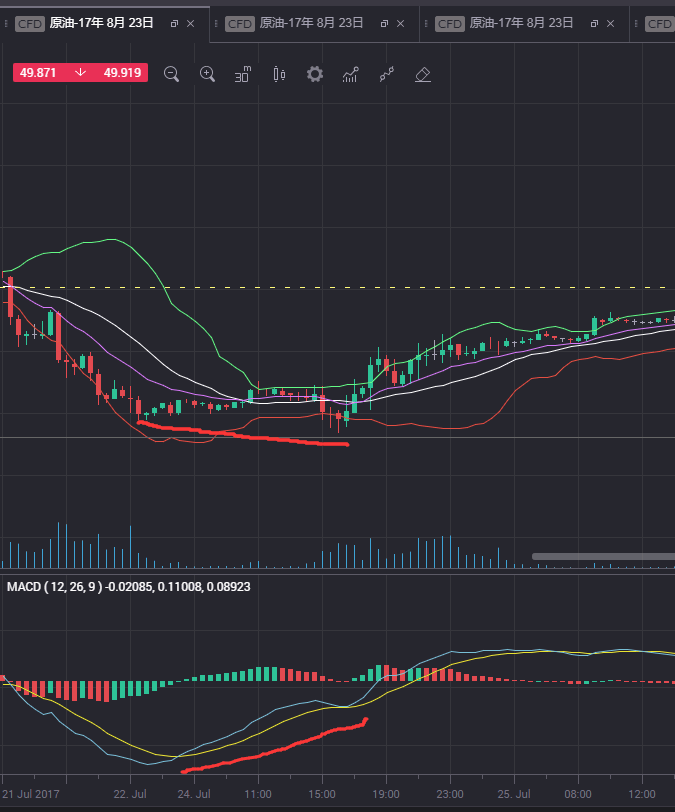
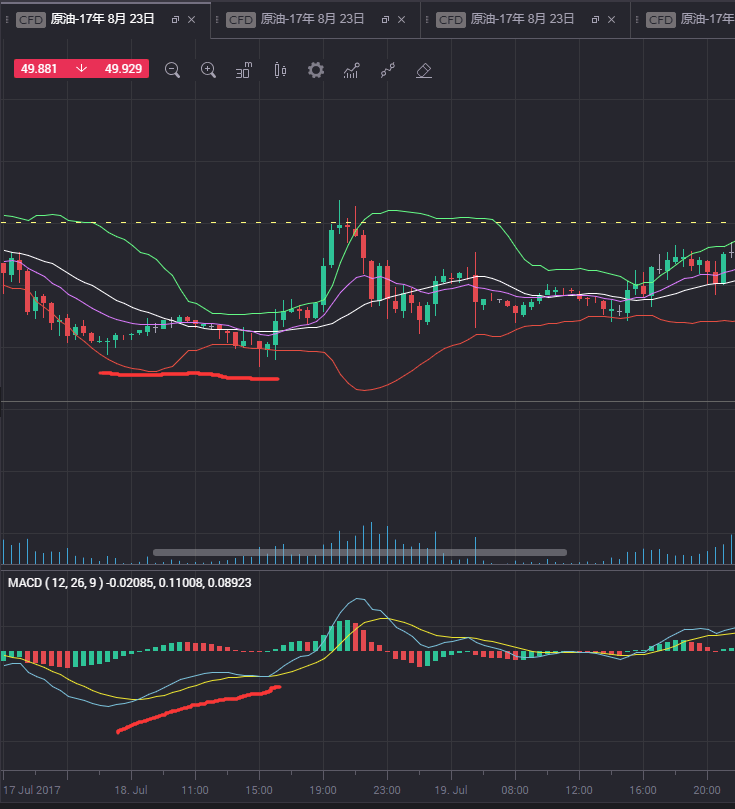
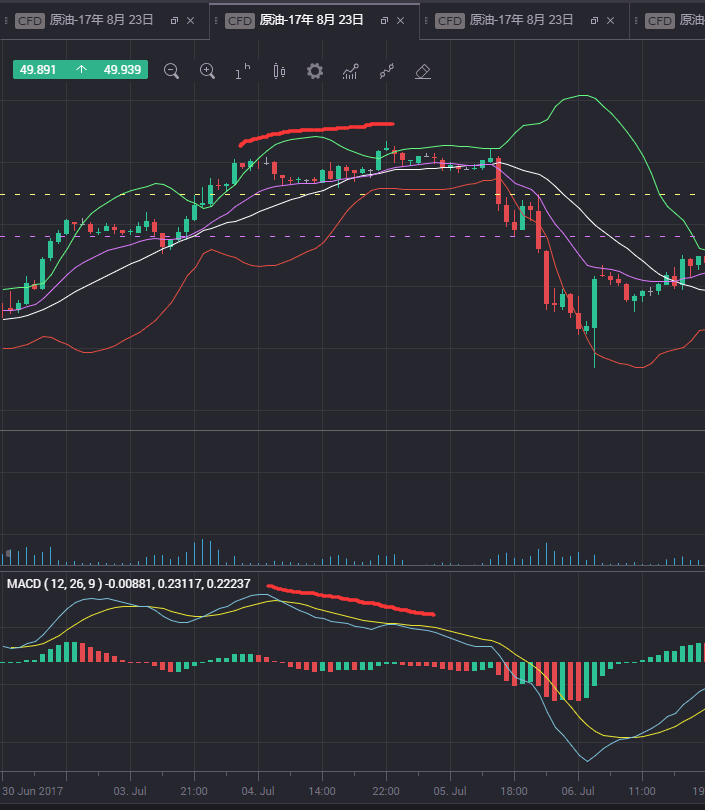
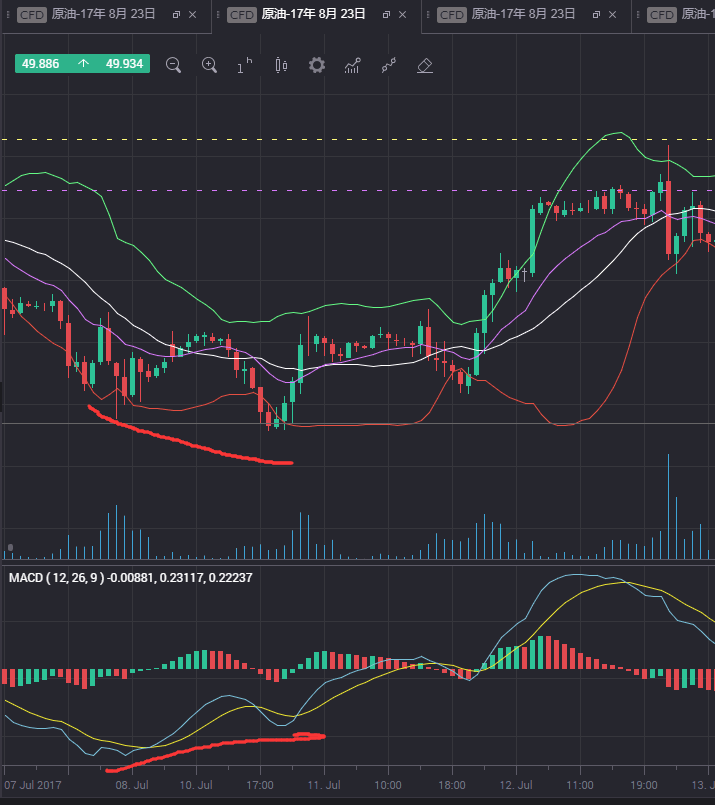
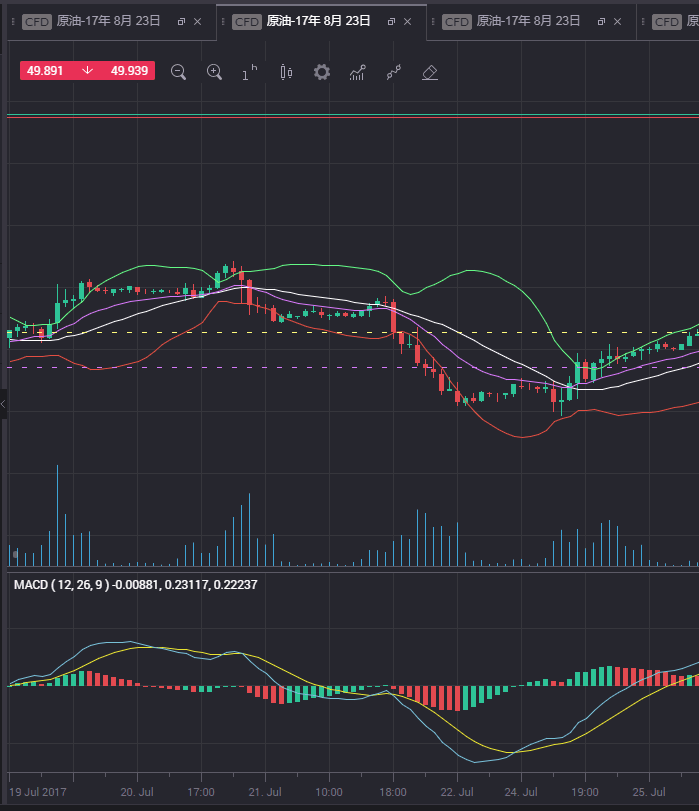
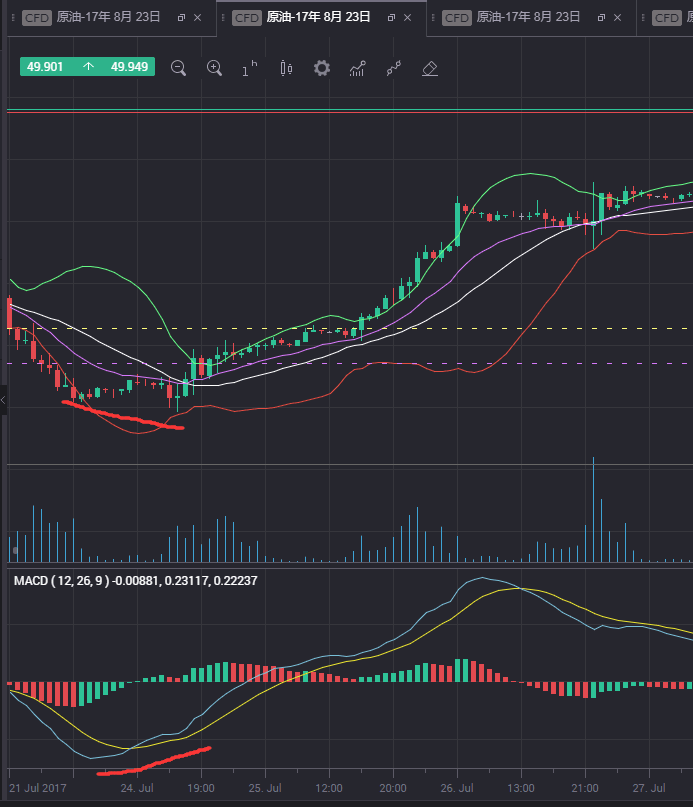
MACD判断定背离，底背离的更多相关文章

  1. MACD底背离选股公式——通达信、同花顺

    {底背离,通达信版.同花顺版} DIFF:=EMA(CLOSE,) - EMA(CLOSE,); DEA:=EMA(DIFF,); MACD:=*(DIFF-DEA); QZQ:=BARSLAST(R ...

  2. 一位交易巨匠的十年心得：如何使用MACD判断后期趋势，把握买卖点

    高手与散户的区别在哪里? 高手与散户的区别在哪里,从宏观上讲:一流高手用境界,二流高手用趋势,三流高手用技术,普通散户用迷糊.最高境界的人在讲心境如何,什么也不看,只用感觉就能炒好股赚钱.我说一流高手 ...

  3. 学习MACD指标

    概念 MACD叫指数平滑异同移动平均线指标. 零轴 MACD柱线 DIFF线 DEA线 使用 一般出现如下情形,股价处于或即将进入上涨趋势中: MACD指标在零轴上方出现金叉,其后DIFF快线一直位于 ...

  4. [转载]MACD 各周期指标状态

    MACD指标:MACD指标是一个非常好用的指标,它与均线.量价关系配合使用对判断行情很有效.这里有必要再深一点讲MACD级别之间的作用. 一.首先,必须明白的是任何指标中都是大级别包含小级别,小级别对 ...

  5. macd背离的级别

    1分钟的背离可以忽略不看. 5分钟的背离可以预测未来5-6个小时的股价. 15分钟级别的背离可以预测未来24小时之内的股价. 30分钟级别的背离可以做中线. 周线背离可以影响1-2年的股价. 背离级别 ...

  6. MACD各分时背离所对应的时间

    MACD各分时背离所对应的时间 5分钟背离结构——2小时.           15分钟背离结构——一天半(6小时).           30分钟背离结构——3天(12小时).            ...

  7. MACD技术的高级应用--MACD与波浪

    在开始分析MACD指标之前,我想我们必须先从思想上认同以下两点,否则本文的研究就没有意义.  1)趋势在一段时间内是可以把握的:  2)每个指标都有有效的时候,没有指标会始终有效.我们就是要搞清楚指标 ...

  8. MACD回零轴有三种方式

    MACD回零轴三种方式 MACD上双线回抽或者回档到0轴附近: 第一主动回零轴. 第二被动回零轴. 第三单N回零轴. 随后的走势第二种涨幅最猛.第三种级别最大. 这里要正确理解背离.背离有三种.1,指 ...

  9. 短线技术MACD指标图解

    1.通常DIF上穿0轴线的当天是中长线难得第一次买入的好时机,会引起场外资金的关注,如果上穿后MACD没有调头的迹象,则股价回调到5日均线附近为买入的好时机,必要时参考其他指标追涨.在0轴线以上形成2 ...

随机推荐

  1. Java 数组的 12 个最佳方法

    1.  声明一个数组 String[] aArray = new String[5]; String[] bArray = {"a","b","c&q ...

  2. 实用ExtJS教程100例-004：等待对话框Ext.MessageBox.wait

    在前面两节中,我们分别演示了ExtJS三种常用的对话框和ExtJS带有进度条的对话框.在本节内容中,我们来看看ExtJS中的等待对话框. 首先来看一个简单的例子[查看在线示例]: 这种对话框会一直滚动 ...

  3. [Web 前端] 如何构建React+Mobx+Superagent的完整框架

    ReactJS并不像angular一样是一个完整的前端框架,严格的说它只是一个UI框架,负责UI页面的展示,如果用通用的框架MVC来说,ReactJs只负责View了,而Angular则是一个完整的前 ...

  4. RAISR: rapid and accurate image super resolution

      准确地说,RAISR并不是用来压缩图像的,而是用来upsample图像的. 众所周知,图片缩小到半分辨率后,在拉回原大小,会出现强烈的锯齿.从80年代开始就有很多super sampling的方法 ...

  5. UEFI与 Legacy BIOS两种启动模式详解

    (1). UEFI启动模式 与 legacy启动模式 legacy启动模式: 就是这么多年来PC一直在使用的启动方式(从MBR中加载启动程序),UEFI BIOS作为一种新的BIOS自然也应该兼容这种 ...

  6. [转]Nginx+mysql+php-fpm负载均衡配置实例

    转 : http://www.jbxue.com/article/7923.html 介绍一个nginx.mysql.php-fpm环境下配置负载均衡的例子,有需要的朋友,可以参考下. 系统环境如下: ...

  7. Reader 与 Guava MultiReader

    Reader是Java IO体系里字符处理读取流的基本类,代码如下 /* * %W% %E% * * Copyright (c) 2006, Oracle and/or its affiliates. ...

  8. 开闭原则(Open Closed Principle，OCP)

    遵循开闭原则设计出的模块具有两个主要特征: 对于扩展是开放的(Open for extension).这意味着模块的行为是可以扩展的.当应用的需求改变时,我们可以对模块进行扩展,使其具有满足那些改变的 ...

  9. K3C官改固件更新frp客户端

    k3c官改1.2 frpc版本是v0.13,本文介绍如何升级到最新版. 1. 下载最新版frp,发布页:https://github.com/fatedier/frp/releases选择mips版, ...

  10. iOS开发调试篇—Print Description of "string"

    Print Description of "string":把 string 的信息输出到控制台.Copy:复制 string 的信息,包含变量名,类名和值.View Value ...