23最小生成树之Kruskal算法

图的最优化问题：最小生成树、最短路径

典型的图应用问题

无向连通加权图的最小生成树

有向/无向加权图的最短路径

四个经典算法

Kruskal算法、Prim算法---------------最小生成树

Dijkstra算法、Floyd算法-------------最短路径

最小生成树的概念:

G=(V,E)：无向连通加权图

C(e)或C(v,w)： 边e=(v,w)的耗费（Cost）

若S=(V,T)是G的一棵生成树（T是树边集）,那么， S的边长之和称作生成树S的耗费C(S)

耗费C(S)达到最小值的生成树S，称为G的最小耗费生成树，也称最小生成树（MinimumSpanningTree）

即C(S)≤C(S') （S'是图G的任一生成树）

注意：最小生成树可能不唯一

Kruskal算法

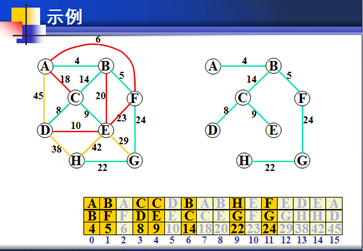
算法思想: 按长度从小到大的依次把边加进生成树,若添加某边后形成了回路，就舍弃这条边

反复如此，直到选出n-1条边，便得到最小生成树.。

通俗来讲，该算法很简单。

步骤：

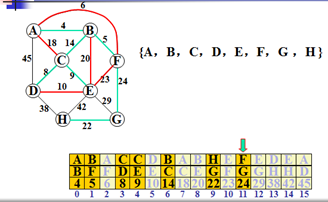
1.在空白处画出与原图一模一样的结点位置。（只画结点，权不需要，结点的位置要一模一样）。

2.按权画边。从权值最小的开始，如图，从4开始，草图就连A-B，到权值5，就连B-F，到权值6，此时就会发现，如果连接A-F，那么A-B-F就会构成一个完整的回路（从任意一点出发可以回到原点。）。因此，就要舍去权值6，即边A-F不可连接。。。。。依次按权大小画其他边。直到最后一个结点。

Kruskal算法伪程序形式

void  Kruskal(***) //***表示函数要求的参数

{  int et=0;           //et用于记录选中的边数

置树边集T为空；

while(et<n-1)               //n是图中的顶点数

{ 从G中选出当前最短边（v，w）；

if(添此边于T中，不使生成树产生回路)

{ 把（v，w）加进T；et++；}

else  舍弃（v，w）；

}

}

实现方法分析：

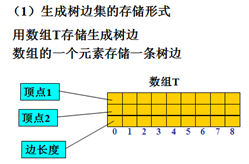
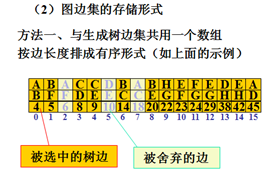
子树合并法描述和示例

描述：

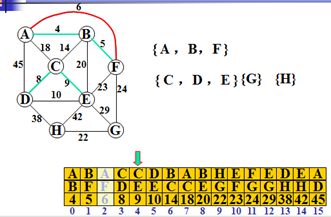
Kruskal算法的子树合并法描述形式：

方法一：

void  Kruskal(***) //***表示函数要求的参数

{  int et=0;

每个顶点自成一个集合，并指定集合名;

while(et<n-1)

{ 从G中选出当前最短边（v，w）;

找到v所在的集合名i，和w所在的集合名j;

if(i!=j)

{  把（v，w）加进T;  et++;

将集合i与集合j合并成一个集合k;     }

}

}

方法二：

void  Kruskal(***) //***表示函数要求的参数

{  int et=0;

每个顶点一个集合，并指定集合名 ;

while(et<n-1)

{ 从G中选出当前最短边（v，w）；

if(v和w不在同一子树中)

{ 把（v，w）加进T；et++；

将v所在的子树与w所在的子树合并成一棵子树;

}

}

}

结论：无论是按权画边法，还是子树合并法都是可以找出最小生成树，但是个人认为按权画边法比较容易理解。