【POJ2778】DNA Sequence 【AC自动机，dp，矩阵快速幂】

题意

题目给出m(m<=10)个仅仅由A,T,C,G组成的单词(单词长度不超过10)，然后给出一个整数n(n<=2000000000)，问你用这四个字母组成一个长度为n的长文本，有多少种组成方法可以使得它不含任何一个给出的单词。

分析

当时一看以为是跟训练指南上（UVA11468）一样的题，感觉只有四个字母并且单词数量和长度也比较小，但是一看给出的n有点懵逼。如果再按照书上建立AC自动机以后直接跑DP的方法肯定是不行了。然后我们就要用到，递推利器，矩阵快速幂。

我们还是按照套路先把AC自动机建出来，然后将每个单词结点设为非法结点，题目变成在AC自动机中走n步不通过非法结点的方案数。然后设f[i][j]是当前在结点i，已经走了j步，且未走过非法结点的方案数。然后怎么转移呢？

f[i][j]=A(0,i)*f[0][j-1]+A(1,i)*f[1][j-1]+...+A(sz-1,i)f[sz-1][j-1]。其中A(i,j)的含义就是从i到j有几条直接连接的边。那么将这个dp方程拆开来看

f0[i]=A(0,0)*f[0][i-1]+A(1,0)*f[1][i-1]+....+A(sz-1,0)*fsz-1[i-1]

f1[i]=A(0,1)*f[0][i-1]+A(1,1)*f[1][i-1]+....+A(sz-1,1)*fsz-1[i-1]

.

.

fsz-1[i]=A(0,sz-1)*f[0][i-1]+A(1,sz-1)*f[1][i-1]+...+A(sz-1,sz-1)*fsz-1[i-1]

然后根据这个我们就很好建立转移矩阵

*

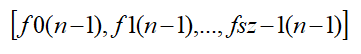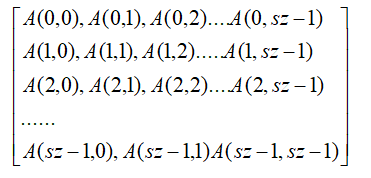
（第一次学会用公式编辑器不过好像还是贼丑）

然后建立这个大的转移矩阵，矩阵的(i,j)为结点i到结点j的直接路径的条数，然后跑一个矩阵快速幂。

最后把从0到sz-1结点的f(n)的值全部加起来就是答案了。

对了这个题需要用long long

下面是代码

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <iostream>
 #include <queue>
 #include <map>

 using namespace std;
 const int maxnode=;
 const int MOD=;
 map<char,int>M;
 struct AC_Automata{
     int ch[maxnode][],f[maxnode],last[maxnode],val[maxnode],match[maxnode];
     int sz;
     int idx(char c){
         return M[c];
     }
     void init(){
         sz=;
         memset(ch[],,sizeof(ch[]));
         memset(match,,sizeof(match));
         val[]=;
     }
     void insert(char *s){
         int n=strlen(s),u=;
         for(int i=;i<n;i++){
             int c=idx(s[i]);
             if(!ch[u][c]){
                 ch[u][c]=sz;
                 memset(ch[sz],,sizeof(ch[sz]));
                 val[sz++]=;
             }
             u=ch[u][c];
         }
         val[u]=;
         match[u]=;
     }
     void getFail(){
         queue<int>q;
         last[]=f[]=;
         for(int i=;i<;i++){
             int u=ch[][i];
             if(u){
                 q.push(u);
                 f[u]=last[u]=;
             }
         }
         while(!q.empty()){
             int r=q.front();q.pop();
             for(int i=;i<;i++){
                 int u=ch[r][i];
                 if(!u){
                     ch[r][i]=ch[f[r]][i];
                     continue;
                 }
                 q.push(u);
                 int v=f[r];
                 while(v&&!ch[v][i])v=f[v];
                 f[u]=ch[v][i];
                 match[u]|=match[f[u]];
             }
         }
     }
 }ac;
 const int maxN=;
 struct Matrix{
     long long a[maxN][maxN];
     void init(){
         memset(a,,sizeof(a));
         for(int i=;i<ac.sz;i++)
             a[i][i]=;
     }
 };
 Matrix mul(Matrix a,Matrix b){
     Matrix res;
     for(int i=;i<ac.sz;i++){
         for(int j=;j<ac.sz;j++){
             res.a[i][j]=;
             for(int k=;k<ac.sz;k++){
                 res.a[i][j]+=a.a[i][k]*b.a[k][j];
                 res.a[i][j]%=MOD;
             }
         }
     }
     return res;
 }
 Matrix qpow(Matrix a,int k){
     Matrix res;
     res.init();
     while(k){
         if(k%)res=mul(res,a);
         a=mul(a,a);
         k/=;
     }
     return res;
 }
 int n,m;
 char s[];

 int main(){
     M['A']=,M['C']=,M['T']=,M['G']=;
     ac.init();
     scanf("%d%d",&m,&n);
     for(int i=;i<=m;i++){
         scanf("%s",s);
         ac.insert(s);
     }
     ac.getFail();
     Matrix A;
     for(int i=;i<ac.sz;i++){
             if(!ac.match[i])
         for(int j=;j<;j++){
             int u=ac.ch[i][j];
             if(!ac.match[u])
             A.a[i][u]++;
         }
     }
     /*for(int i=0;i<ac.sz;i++){
         for(int j=0;j<ac.sz;j++){
             printf("%d ",A.a[i][j]);
         }
         printf("\n");
     }*/

     Matrix S;
     S.a[][]=;
     Matrix ANS;
     ANS=qpow(A,n);
     ANS=mul(S,ANS);
     long long ans=;
     for(int i=;i<=ac.sz;i++)
         ans+=ANS.a[][i];
     printf("%d\n",ans%MOD);
 return ;
 }