【ACM】 1231 最大连续子序列

[1231 最大连续子序列
**
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 38975 Accepted Submission(s): 17603
**
浙大计算机研究生复试上机考试-2005年

---

要勾选c++才能过；
题意：输入一串数列，输出该数列的最大连续子序列（不能间隔），以及该最大连续子序列的第一个和最后一个元素。
EG：-2 11 -4 13 -5 -2
output 11+（-4）+13=20
思路：用数组temp[]存储输入的数列；
定义两个变量（maxLeft maxRight)保存最大连续子序列的 最左最右两个元素（第一和最后一个元素）在原数列的下标；
maxSum表示最大的和；
thisSum当前正在遍历 的子序列的和；
thisLeft当前正在遍历 的子序列的最左边的元素。

难点：如何区分那些元素在最大连续子序列中？最大和？
其实很简单，先让maxSum=temp[0],如果thisSum<0，舍弃当前遍历的子序列，进入下一个新的子序列，每次进入下一子序列时thisSum=0,
（EG：-1 4 -2 -1 -7 9 -1 3）
分成了3个连续子序列。而最大连续子序列可能是子序列的子序列。

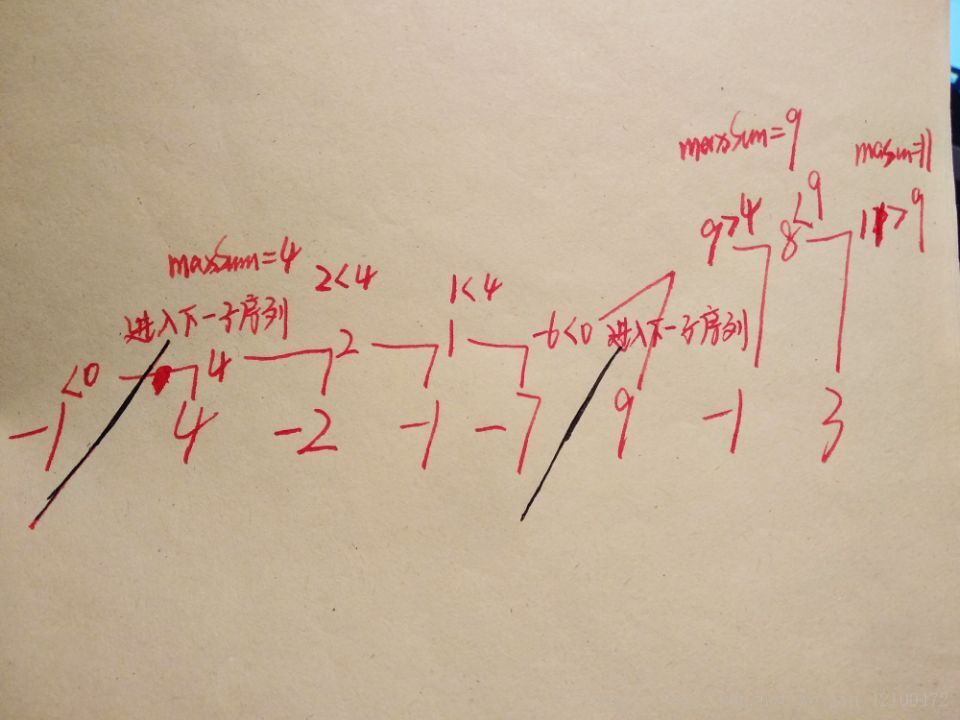
如何记录 子序列的第一和最后一个元素？
每次thisSum<0时，记录下一元素角标为thisLeft；
当thisSum为当前最大和时，maxLeft=thisLeft,maxRight=i(for循环里的局部变量，控制次数）

注意：
必须 有memset(temp,0,sizeof(temp));初始化，不然输出的结果有时候是错误的。

#include <stdio.h>
#include<string>

int main()
{
    int  n, maxLeft, maxRight, maxSum, temp[10005];
    int thisLeft, thisSum;
    while(scanf("%d", &n)!=EOF&&n)
    {
        memset(temp,0,sizeof(temp));
        scanf("%d", &temp[0]);
        thisLeft = maxLeft = maxRight =  0;
        maxSum=temp[0];
        thisSum = maxSum;
        if(thisSum < 0)
        {
            thisSum = 0; thisLeft = 1;
        }
        for(int i = 1; i < n; ++i)
        {
            scanf("%d", &temp[i]);
            thisSum += temp[i];
            if(thisSum > maxSum)
            {
                maxSum = thisSum;
                maxLeft = thisLeft;
                maxRight = i;
            }
            if(thisSum < 0)
            {
                thisLeft = i + 1;
                thisSum = 0;
            }
        }
        if(maxSum>=0)
        printf("%d %d %d\n", maxSum,temp[maxLeft], temp[maxRight]);
        else
            printf("%d %d %d\n", 0,temp[0], temp[n-1]);

    }
    return 0;
}