论文解读（GraphMAE）《GraphMAE: Self-Supervised Masked Graph Autoencoders》

论文信息

论文标题：GraphMAE: Self-Supervised Masked Graph Autoencoders
论文作者：Zhenyu Hou, Xiao Liu, Yukuo Cen, Yuxiao Dong, Hongxia Yang, Chunjie Wang, Jie Tang
论文来源：2022, KDD
论文地址：download 
论文代码：download

1 Introduction

　　GAE 研究困难之处：

• 首先，过度强调结构信息。
  • 大多数 GAEs 利用重建边连接作为目标来鼓励邻居 [3,17,20,26,31,42] 之间的拓扑紧密性。该类型方法适用与链路预测和节点聚类，对节点和图分类却不令人满意。
• 其次，无损坏的特征重构可能不够健壮。
  • GAEs[3,20,26,27,31]，大多使用有风险学习琐碎解决方案的普通体系结构。
• 第三，均方误差(MSE)可能是敏感的和不稳定的。
  • 现有的具有特征重建 [17,18,27,31,42] 的 GAEs 都采用了 MSE 作为标准，没有额外的预防措施。然而，已知 MSE 存在不同的特征向量范数和维数[5] 的诅咒，因此可能导致自动编码器训练的崩溃。
• 第四，解码器的架构很少有表现力。
  
  • 大多数 [3、16-18、20、26、42] 利用MLP作为解码器。由于图中大多数节点所含的信息较少，使用普通的 MLP 解码器可能无法弥补编码器的表示和解码器目标之间的差距。

2 Method

　　整体框架：

　　

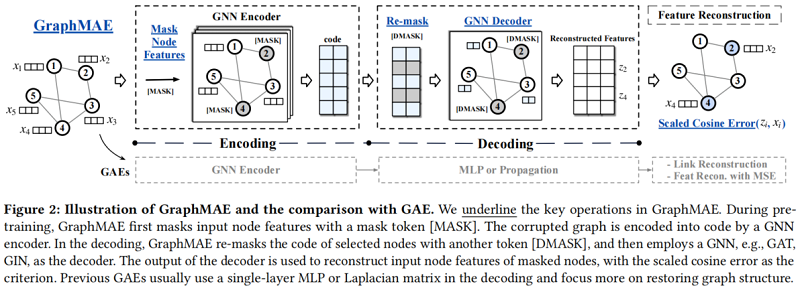
　　核心思想：重构掩蔽节点特征。

　　引入：

• • Q1: What to reconstruct in GAEs?　　
  • Q2: How to train robust GAEs to avoid trivial solutions?　　
  • Q3: How to arrange the decoder for GAEs?　　
  • Q4: What error function to use for reconstruction?　　

2.1 Details

Q1: Feature reconstruction as the objective

　　重建特征信息，不考虑结构信息，Graph-less Neural Networks [58] 也证明了 MLP 在节点分类中的强大。

Q2: Masked feature reconstruction

　　自编码器容易陷入 “identity function” (恒等映射)的问题[41]。对于图像等高维数据，这不是一个严重的问题，但是对于图数据来说，其维度相对较小，所以效果并不是很好[3, 20, 26, 27, 31]。

　　本文采用掩码自动编码器作为 GraphMAE 的主干。

　　形式上，采样节点子集 $\tilde{\mathcal{V}} \subset \mathcal{V}$，并使用一个掩码标记（mask token）[MASK] 来掩盖该节点子集每个节点的特征，即一个可学习的向量 $x_{[M]} \in \mathbb{R}^{d}$。因此，掩蔽特征矩阵 $\widetilde{X}$ 可以定义为：

　　　　$\tilde{x}_{i}=\left\{\begin{array}{ll}x_{[M]} & v_{i} \in \widetilde{\mathcal{V}} \\x_{i} & v_{i} \notin \widetilde{\mathcal{V}}\end{array}\right.$

　　GraphMAE的目标是通过给定部分观测到的节点特征矩阵 $\widetilde{X}$ 和输入邻接矩阵 $A$，重构 $\widetilde{V}$ 中节点特征矩阵。

　　本文采用统一的随机抽样策略来掩蔽节点，均匀分布的随机抽样使得一个节点的邻居既不是都是掩盖的，也不是全部可见的，这有助于防止潜在的偏置中心。本文考虑了一个较大的掩蔽率，以减少属性图中的冗余。

　　另一方面，[MASK] 的使用可能会造成训练和推理之间的不匹配，因为 [MASK] 标记在推理[49]过程中不会出现。本文实验发现，“leave-unchanged”的策略实际上损害了GraphMAE的学习，而 “random-substitution” 的方法可以帮助形成更多高质量的表征。

Q3: GNN decoder with re-mask decoding

　　由于 MLP 的“identity function” 问题，所以本文使用单层GNN作为其解码器。GNN解码器可以基于一组节点而不仅仅是节点本身来恢复一个节点的输入特征，从而帮助编码器学习高级潜在代码。

　　为提高解码器解码潜在表示，本文提出一种 re-mask decoding 技术来处理潜在表示 $H$。即，对 Encoder 中的掩蔽节点再次进行 mask token [DMASK] 处理，也就是$\boldsymbol{h}_{[M]} \in \mathbb{R}^{d_{h}}$。具体来说，重新掩码的 潜在表示 $\widetilde{H}=\operatorname{REMASK}(H)$  为：

　　　　$\tilde{\boldsymbol{h}}_{i}=\left\{\begin{array}{ll}\boldsymbol{h}_{[M]} & v_{i} \in \widetilde{V} \\\boldsymbol{h}_{i} & v_{i} \notin \widetilde{\mathcal{V}}\end{array}\right.$

　　实证检验表明，GAT 和 GIN 编码器分别是节点分类和图分类的良好选择。解码器只在自监督训练阶段使用，因此可以选择任意类型的GNN解码器。

Q4: Scaled cosine error as the criterion

　　对于特征重建的 MSE 损失，由于在最小化接近 $0$ 的时候很难优化，所以GraphMAE采用了余弦误差来度量重建效果。同时，引入可放缩的余弦误差（Scaled Cosine Error）来进一步改进余弦误差。

　　本文设置 $\gamma>1$ ，好处是当置信度高的时候，误差将快速收敛到 $0$，从而调整了不同样本的权重。给定原始特征矩阵 $X$ 和解码器输出 $Z=f_{D}(A, \widetilde{H})$，放缩的余弦误差的定义为：

　　　　$L=\frac{1}{|\widetilde{\mathcal{V}}|}\left(1-\frac{x_{i}^{T} z_{i}}{\left\|x_{i}\right\| \cdot\left\|z_{i}\right\|}\right)^{\gamma}, \gamma \geq 1$

　　放缩因子 $\gamma$ 是一个在不同数据集上可调整的超参数，可以被看作是一种自适应的样本权重调整，每个样本的权重随着重建误差的不同进行调整。某种程度上类似于Focal Loss [22]。

　　Figure 1 是架构设计对比：

　　

2.2 Training and Inference

　　首先，给定一个输入图，我们随机选择一定比例的节点，并用掩模标记[MASK]替换它们的节点特征。我们将具有部分观察到的特征的图输入编码器，以生成编码的节点表示。在解码过程中，我们重新掩码所选的节点，并用另一个标记[DMASK]替换它们的特性。然后将解码器应用于重新掩码图，利用所提出的尺度余弦误差重建原始节点特征。

　　对于下游应用程序，编码器应用于输入图，在推理阶段没有任何掩蔽。生成的节点嵌入可用于各种图学习任务，如节点分类和图分类。对于图形级的任务，我们使用一个非参数化的图池化（READOUT）函数，例如，MaxPooling，MeanPooling，以获得图形级的表示 $\boldsymbol{h}^{g}=\operatorname{READOUT}\left(\left\{\boldsymbol{h}_{i}, v_{i} \in \mathcal{G}_{g}\right\}\right)$。此外，与[16]类似，GraphMAE还能够将预先训练过的GNN模型鲁棒地转移到各种下游任务中。在实验中，我们证明了GraphMAE在节点级和图级应用中都具有竞争力的性能。

3 Experiments

3.1 Node classificatio

　　 

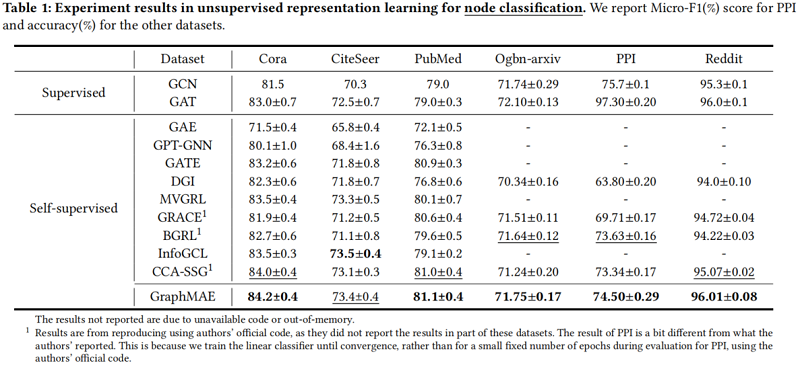
3.2 Graph classification

　　

3.3 Transfer learning on molecular property prediction

　　

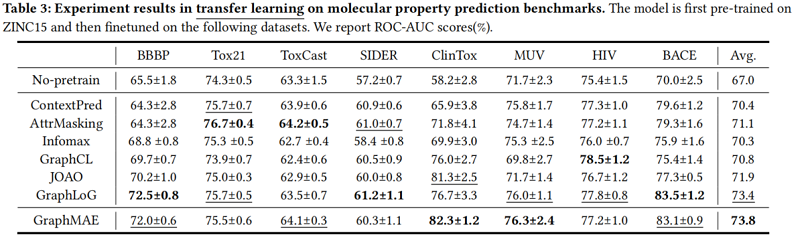
3.4 Ablation Studies

Effect of reconstruction criterion & Effect of mask and re-mask

　　

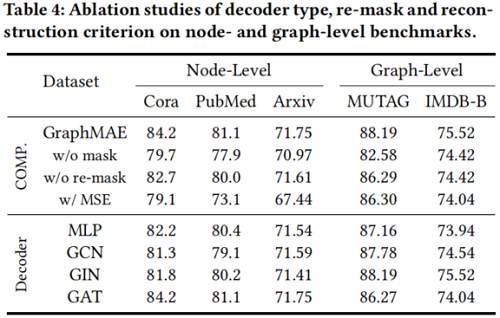
Effect of mask ratio

　　

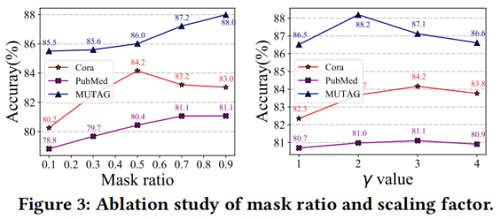
Effect of decoder type

　　

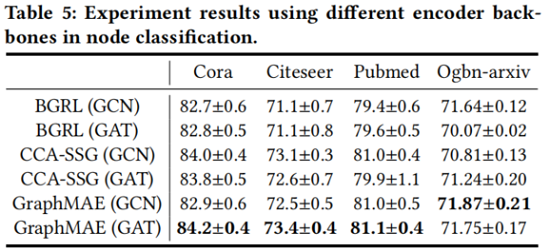
4 Conclusion

　　贡献：

• • MAE 思想用于图上；
  • 提出一种放缩余弦误差；

修改历史

2022-06-17 创建文章

论文解读目录