采用C++实现哈夫曼树的创建并输出哈夫曼编码

一、问题源自一道信息论的作业题：

二、完整代码如下  1 #include <iostream>

 #include <string>
 #include <deque>
 #include <algorithm>
 using namespace std;
 struct Node{
     Node *parent, *lchild, *rchild;
     pair<float, string> value;
 };
 class Tree{
 public:
     int max;
     deque<pair<float, string>> leafs; //存放所有叶子
     Node *root;
     void hfTree();                                //将所有叶子组合成哈夫曼树
     Tree(deque<pair<float, string>>);             //构造函数
     bool findLeaf(const pair<float, string> &);   //查找叶子
     bool deleteLeaf(const pair<float, string> &); //删除叶子
     void sortLeafs();
 };
 //重载pair的加法运算
 pair<float, string> operator+(pair<float, string> pr1, pair<float, string> pr2){
     return pair<float, string>(pr1.first + pr2.first, pr1.second + pr2.second);
 }
 //Tree的构造函数
 Tree::Tree(deque<pair<float, string>> lf){
     int count = ;
     for (deque<pair<float, string>>::iterator it = lf.begin(); it != lf.end(); it++){
         this->leafs.push_front(*it);
         count++;
     }
     this->max = count;
     this->root = NULL;
 } //根据键值对判断是否存在该叶子
 bool Tree::findLeaf(const pair<float, string> &pr){
     for (deque<pair<float, string>>::iterator it = this->leafs.begin(); it != this->leafs.end(); it++){
         if ((*it) == pr){
             return true;
         }
     }
     return false;
 }
 //根据键值对删除一个叶子
 bool Tree::deleteLeaf(const pair<float, string> &pr){
     for (deque<pair<float, string>>::iterator it = this->leafs.begin(); it != this->leafs.end(); it++){
         if ((*it) == pr){
             pair<float, string> temp = this->leafs.back();
             while (temp != (*it)){
                 this->leafs.pop_back();
                 this->leafs.push_front(temp);
                 temp = this->leafs.back();
             }
             this->leafs.pop_back();
             return true;
         }
     }
     return false;
 }
 //删除deque<Node*>中的一个元素
 void deleteNode(deque<Node *> &temp, const pair<float, string> &pr){
     for (deque<Node *>::iterator it = temp.begin(); it != temp.end(); it++){
         if ((*it)->value == pr){
             Node *nd = temp.back();
             while (nd->value != pr){
                 temp.pop_back();
                 temp.push_front(nd);
                 nd = temp.back();
             }
             temp.pop_back();
             return;
         }
     }
 }
 //根据键值对找到节点并返回其地址
 Node *findNode(deque<Node *> &temp, const pair<float, string> &pr){
     for (deque<Node *>::iterator it = temp.begin(); it != temp.end(); it++){
         if ((*it)->value == pr){
             return *it;
         }
     }
     return NULL;
 }
 bool isIn(deque<Node *> &temp, const pair<float, string> &pr){
     for (deque<Node *>::iterator it = temp.begin(); it != temp.end(); it++){
         if ((*it)->value == pr){
             return true;
         }
     }
     return false;
 }
 //根据所存的叶子节点构造哈夫曼树
 void Tree::hfTree(){
     deque<Node *> temp;
     temp.push_front(NULL);
     while (this->leafs.begin() != this->leafs.end()){
         //对所有叶子排序并取出概率最小的两个叶子节点
         this->sortLeafs();
         pair<float, string> pr1;
         pair<float, string> pr2;
         if (this->leafs.back() == this->leafs.front()){//只剩一个叶子了
             pr1 = pr2 = this->leafs.front();
             this->leafs.pop_front();
         }else{
             pr1 = this->leafs.front();
             this->leafs.pop_front();
             pr2 = this->leafs.front();
             this->leafs.pop_front();
         }
         //首次合并，特殊处理
         if (temp.front() == NULL){
             temp.pop_front();
             Node *node = new Node;
             if (pr1 == pr2){
                 node->lchild = node->parent = node->rchild = NULL, node->value = pr1;
             }else{
                 Node *node1 = new Node;
                 Node *node2 = new Node;
                 node1->value = pr1, node2->value = pr2, node->value = pr1 + pr2;
                 node1->lchild = node1->rchild = node2->rchild = node2->lchild = node->parent = NULL;
                 node1->parent = node2->parent = node, node->lchild = node1, node->rchild = node2;
             }
             this->leafs.push_front(node->value);
             temp.push_front(node);
         }else{
             Node *node = new Node;
             if (pr1 == pr2){//只剩一个节点了而且是被处理过的，表明所有节点处理完毕，直接退出
                 break;
             }else{//新选出的两个节点都是已经处理后得到的根节点
                 if (isIn(temp, pr1) && isIn(temp, pr2)){
                     Node *node1 = findNode(temp, pr1);
                     Node *node2 = findNode(temp, pr2);
                     node->value = pr1 + pr2;
                     node->parent = NULL;
                     node1->parent = node2->parent = node, node->lchild = node1, node->rchild = node2;
                     this->deleteLeaf(pr1), this->deleteLeaf(pr2), deleteNode(temp, pr1), deleteNode(temp, pr2); //删除选出来的两个节点
                     this->leafs.push_front(node->value);
                 }else if (isIn(temp, pr1)){
                     Node *tp = findNode(temp, pr1);
                     Node *node2 = new Node;
                     node2->value = pr2, node->value = pr1 + pr2;
                     node2->rchild = node2->lchild = node->parent = NULL;
                     node2->parent = tp->parent = node, node->rchild = node2, node->lchild = tp;
                     this->deleteLeaf(pr1), this->deleteLeaf(pr2);               //删除选出来的节点
                     this->leafs.push_front(node->value), deleteNode(temp, pr1); //将合并的节点放到生成树和原始集合中
                 }else if (isIn(temp, pr2)){
                     Node *tp = findNode(temp, pr2);
                     Node *node1 = new Node;
                     node1->value = pr1, node->value = pr1 + pr2;
                     node1->rchild = node1->lchild = node->parent = NULL;
                     node1->parent = tp->parent = node, node->lchild = node1, node->rchild = tp;
                     this->deleteLeaf(pr1), this->deleteLeaf(pr2);               //删除选出来的节点
                     this->leafs.push_front(node->value), deleteNode(temp, pr2); //将合并的节点放到生成树和原始集合中
                 }else{
                     Node *node1 = new Node;
                     Node *node2 = new Node;
                     node->value = pr1 + pr2;
                     node->parent = NULL;
                     node1->value = pr1, node2->value = pr2;
                     node1->parent = node2->parent = node, node->lchild = node1, node->rchild = node2;
                     node1->lchild = node2->lchild = node1->rchild = node2->rchild = node->parent = NULL;
                     this->deleteLeaf(pr1), this->deleteLeaf(pr2); //删除选出来的两个节点
                     this->leafs.push_front(node->value);
                 }
             }
             temp.push_front(node);
         }
     }
     this->root = temp.front();
 }

 //前序遍历一棵树
 void prelook(Node *root,string str){
     if (root != NULL){
         if (root->lchild == NULL && root->rchild == NULL){
             cout << "weight:\t" << root->value.first << "\tcontent:\t" << root->value.second << "\tcode:\t"<<str<<endl;
         }
         if (root->lchild != NULL){
             str+="";
             prelook(root->lchild,str);
             str.pop_back();
         }
         if (root->rchild != NULL){
             str+="";
             prelook(root->rchild,str);
             str.pop_back();
         }
     }
 }
 //重载操作符，实现两个集合的笛卡儿积
 Tree operator+(Tree tr1, Tree tr2){
     deque<pair<float, string>> temp;
     for (deque<pair<float, string>>::iterator it1 = tr1.leafs.begin(); it1 != tr1.leafs.end(); it1++){
         for (deque<pair<float, string>>::iterator it2 = tr2.leafs.begin(); it2 != tr2.leafs.end(); it2++){
             temp.push_back(pair<float, string>((*it1).first * (*it2).first, (*it1).second + (*it2).second));
         }
     }
     return Tree(temp);
 }
 //对一棵树的叶子节点进行排序
 void Tree::sortLeafs(){
     sort(this->leafs.begin(), this->leafs.end());
 }
 int main(){
     deque<pair<float, string>> temp;
     temp.push_front(pair<float, string>(0.5, "a1"));
     temp.push_front(pair<float, string>(0.3, "a2"));
     temp.push_front(pair<float, string>(0.2, "a3"));
     Tree tr = Tree(temp)+Tree(temp)+Tree(temp);
     tr.hfTree();
     prelook(tr.root,"");
     system("pause");
     return ;
 }

三、修改源代码第276行可以实现对任意次方笛卡尔积结果的编码，第三问输出结果如下：

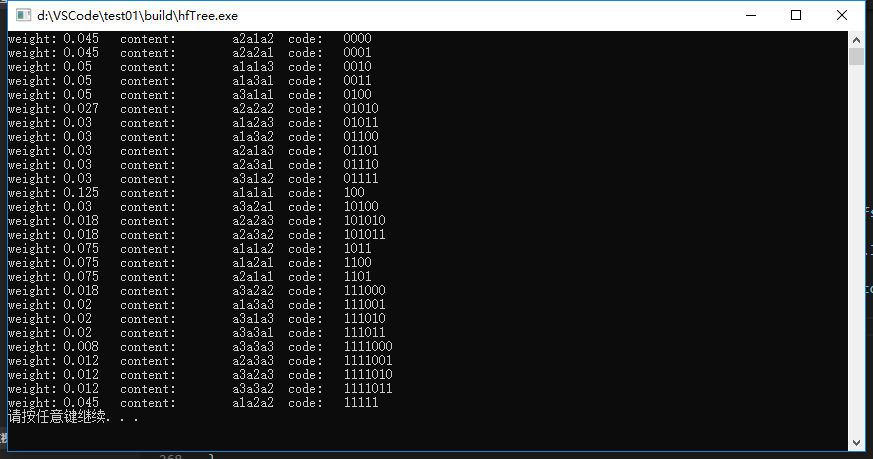
 //表明只剩一个叶子了