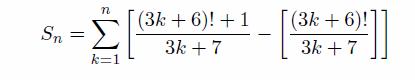hdu2973-YAPTCHA-(欧拉筛+威尔逊定理+前缀和)
YAPTCHA
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1490 Accepted Submission(s):
811
Due to immense amount of unsolicited automated programs which were crawling
across their pages, they decided to put
Yet-Another-Public-Turing-Test-to-Tell-Computers-and-Humans-Apart on their
webpages. In short, to get access to their scientific papers, one have to prove
yourself eligible and worthy, i.e. solve a mathematic
riddle.
However, the test turned out difficult for some math PhD
students and even for some professors. Therefore, the math department wants to
write a helper program which solves this task (it is not irrational, as they are
going to make money on selling the program).
The task that is presented
to anyone visiting the start page of the math department is as follows: given a
natural n, compute
where [x] denotes the
largest integer not greater than x.
<= 10^6). Each query consist of one natural number n (1 <= n <=
10^6).
Sn.
1
2
3
4
5
6
7
8
9
10
100
1000
10000
1
1
2
2
2
2
3
3
4
28
207
1609
#include <iostream>
#include<stdio.h>
#include <algorithm>
#include<string.h>
#include<cstring>
#include<math.h>
#define inf 0x3f3f3f3f
#define ll long long
using namespace std;
const int maxx=;
int prime[];
bool vis[];
int ans[];
int cnt; void init()
{
cnt=;
memset(vis,true,sizeof(vis));
vis[]=vis[]=false;
for(int i=;i<=maxx;i++)//欧拉筛
{
if(vis[i])
prime[cnt++]=i;
for(int j=;j<cnt && prime[j]*i<=maxx;j++)
{
vis[ prime[j]*i ]=false;
if( i%prime[j]== ) break;
}
}
memset(ans,,sizeof(ans));
int p;
for(int k=;k<=;k++)
{
p=*k+;
if(vis[p])
ans[k]=ans[k-]+;
else
ans[k]=ans[k-];
}
} int main()///hdu2973,威尔逊定理+前缀和
{
init();
int t,n;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
printf("%d\n",ans[n]);
}
return ;
}
hdu2973-YAPTCHA-(欧拉筛+威尔逊定理+前缀和)的更多相关文章
- UVA12995 Farey Sequence [欧拉函数,欧拉筛]
洛谷传送门 Farey Sequence (格式太难调,题面就不放了) 分析: 实际上求分数个数就是个幌子,观察可以得到,所求的就是$\sum^n_{i=2}\phi (i)$,所以直接欧拉筛+前缀和 ...
- 【BZOJ 2190】【SDOI 2008】仪仗队 欧拉筛
欧拉筛模板题 #include<cstdio> using namespace std; const int N=40003; int num=0,prime[N],phi[N]; boo ...
- [51NOD1181]质数中的质数(质数筛法)(欧拉筛)
题目链接:http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1181 思路:欧拉筛出所有素数和一个数的判定,找到大于n的最小质 ...
- 素数筛&&欧拉筛
折腾了一晚上很水的数论,整个人都萌萌哒 主要看了欧拉筛和素数筛的O(n)的算法 这个比那个一长串英文名的算法的优势在于没有多次计算一个数,也就是说一个数只筛了一次,主要是在%==0之后跳出实现的,具体 ...
- 欧拉筛,线性筛,洛谷P2158仪仗队
题目 首先我们先把题目分析一下. emmmm,这应该是一个找规律,应该可以打表,然后我们再分析一下图片,发现如果这个点可以被看到,那它的横坐标和纵坐标应该互质,而互质的条件就是它的横坐标和纵坐标的最大 ...
- pku-2909 (欧拉筛)
题意:哥德巴赫猜想.问一个大于2的偶数能被几对素数对相加. 思路:欧拉筛,因为在n<215,在3万多,一个欧拉筛得时间差不多4*104, 那么筛出来的素数有4千多个,那么两两组合直接打表,时间复 ...
- hdu2421-Deciphering Password-(欧拉筛+唯一分解定理+积性函数+立方求和公式)
Deciphering Password Time Limit: 5000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Oth ...
- POJ-3126.PrimePath(欧拉筛素数打表 + BFS)
给出一篇有关素数线性筛和区间筛的博客,有兴趣的读者可以自取. 本题大意: 给定两个四位的素数,没有前导零,每次变换其中的一位,最终使得两个素数相等,输出最小变换次数.要求变换过程中的数也都是素数. 本 ...
- 欧拉筛(线性筛) & 洛谷 P3383 【模板】线性筛素数
嗯.... 埃氏筛和欧拉筛的思想都是相似的: 如果一个数是素数,那么它的所有倍数都不是素数.... 这里主要介绍一下欧拉筛的思路:(欧拉筛的复杂度大约在O(n)左右... 定义一个prime数组,这个 ...
随机推荐
- union与union all的用法给区别
用法: 当我们需要把两个或多个sql联合起来查询就用到了union或者union all 区别: 这两者的区别就在于union会自动的把多个sql查出来重复的排除掉,而union all这是会全部显示 ...
- 2-Zookeeper、HA安装
1.Zookeeper安装 1.解压 zookeeper 到安装目录中/opt/app/zookeeper 中. 2.在安装目录下创建data和logs两个目录用于存储数据和日志: cd /opt/a ...
- WPF 选择电脑文件显示路径,弹出资源管理器,打开文件
选择文件,将路径显示在名为txbx的textbox上 // 在WPF中, OpenFileDialog位于Microsoft.Win32名称空间 Microsoft.Win32.OpenFileDia ...
- 关于oracle中varchar2与nvarchar2的一点认识
今天在oracle 10g下测试了下varchar2与nvarchar2这两种类型,网上有很多关于这两种类型的区别的帖子,我还是自己测试了下. varchar2(size type),size最大为4 ...
- Linux NTP
1.Server 2.QuickStart last 1.Server 0.cn.pool.ntp.org 1.cn.pool.ntp.org 2.cn.pool.ntp.org 3.cn.pool. ...
- 部署django项目,sqlite3数据库出错sqlite3.NotSupportedError: URIs not supported
如果遇到这个错误 sqlite3.NotSupportedError: URIs not supported 修改类似 该路径 的 base.py文件 /root/.virtualenvs/fkPy3 ...
- [Unity基础]镜头管理类
一个游戏中可能会有各种类型的镜头,例如有时候是第一人称,有时是第三人称,有时又会给个特写等等,因此可以定义一个镜头类型枚举,在不同的场合进行切换,管理起来很方便. CameraManager.cs u ...
- <转载> bat 脚本基本语法 http://blog.csdn.net/bluedusk/article/details/1500629
bat 脚本基本语法 2007-01-25 10:31 常用命令 echo.@.call.pause.rem(小技巧:用::代替rem)是批处理文件最常用的几个命令,我们就从他们开始学起. = ...
- Oracle查询表结果添加到另一张表中
转自:https://blog.csdn.net/lx870576109/article/details/78336695 把每一个知识点进行积累:Oracle数据库中将查询一张表的结果添加到另一张表 ...
- ABAP-定时-异步
*&---------------------------------------------------------------------* *& Report ZRICO_TES ...