【11】python 递归,深度优先搜索与广度优先搜索算法模拟实现

一、递归原理小案例分析
(1)# 概述
递归:即一个函数调用了自身,即实现了递归 凡是循环能做到的事,递归一般都能做到!
(2)# 写递归的过程
1、写出临界条件
2、找出这一次和上一次关系
3、假设当前函数已经能用,调用自身计算上一次的结果,再求出本次的结果
(3)案例分析:求1+2+3+...+n的数和
# 概述
'''
递归:即一个函数调用了自身,即实现了递归
凡是循环能做到的事,递归一般都能做到! ''' # 写递归的过程
'''
1、写出临界条件
2、找出这一次和上一次关系
3、假设当前函数已经能用,调用自身计算上一次的结果,再求出本次的结果
''' # 问题:输入一个大于1 的数,求1+2+3+....
def sum(n):
if n==1:
return 1
else:
return n+sum(n-1) n=input("请输入:")
print("输出的和是:",sum(int(n))) '''
输出:
请输入:4
输出的和是: 10
'''

#__author:"吉*佳"
#date: 2018/10/21 0021
#function: import os
def getAllDir(path):
fileList = os.listdir(path)
print(fileList)
for fileName in fileList:
fileAbsPath = os.path.join(path,fileName)
if os.path.isdir(fileAbsPath):
print("$$目录$$:",fileName)
getAllDir(fileAbsPath)
else:
print("**普通文件!**",fileName)
# print(fileList)
pass getAllDir("G:\\")
输出结果如下:


二、深度遍历与广度遍历
(一)、深度优先搜索
说明:深度优先搜索借助栈结构来进行模拟
深度遍历示意图:
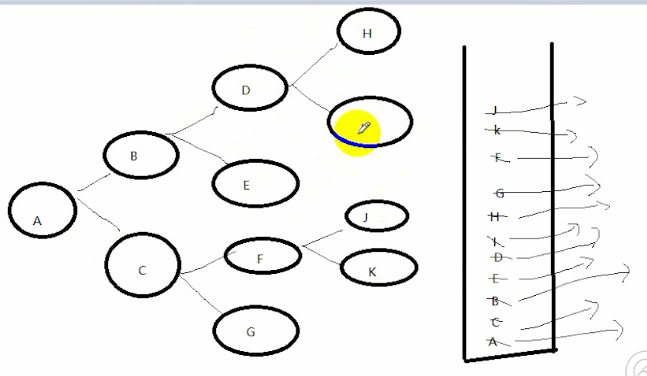
说明:
先把A压栈进去,在A出栈的同时把B C压栈进去,此时让B出栈的同时把DE压栈(C留着先不处理) 同理,在D出栈的时候,H I压栈,最后再从上往下
取出栈内还未出栈的元素,即达到深度优先遍历。
案例实践:利用栈来深度搜索打印出目录结构

程序代码:
#__author:"吉**"
#date: 2018/10/21 0021
#function: # 深度优先遍历目录层级结构 import os def getAllDirDP(path):
stack = []
# 压栈操作,相当于图中的A压入
stack.append(path) # 处理栈,当栈为空的时候结束循环
while len(stack) != 0:
#从栈里取数据,相当于取出A,取出A的同时把BC压入
dirPath = stack.pop()
firstList = os.listdir(dirPath)
#判断:是目录压栈,把该目录地址压栈,不是目录即是普通文件,打印
for filename in firstList:
fileAbsPath=os.path.join(dirPath,filename)
if os.path.isdir(fileAbsPath):
#是目录就压栈
print("目录:",filename)
stack.append(fileAbsPath)
else:
#是普通文件就打印即可,不压栈
print("普通文件:",filename) getAllDirDP(r'E:\[AAA](千)全栈学习python\18-10-21\day7\temp\dir')
结果:

该过程示意图解释:(s-05-1部分)
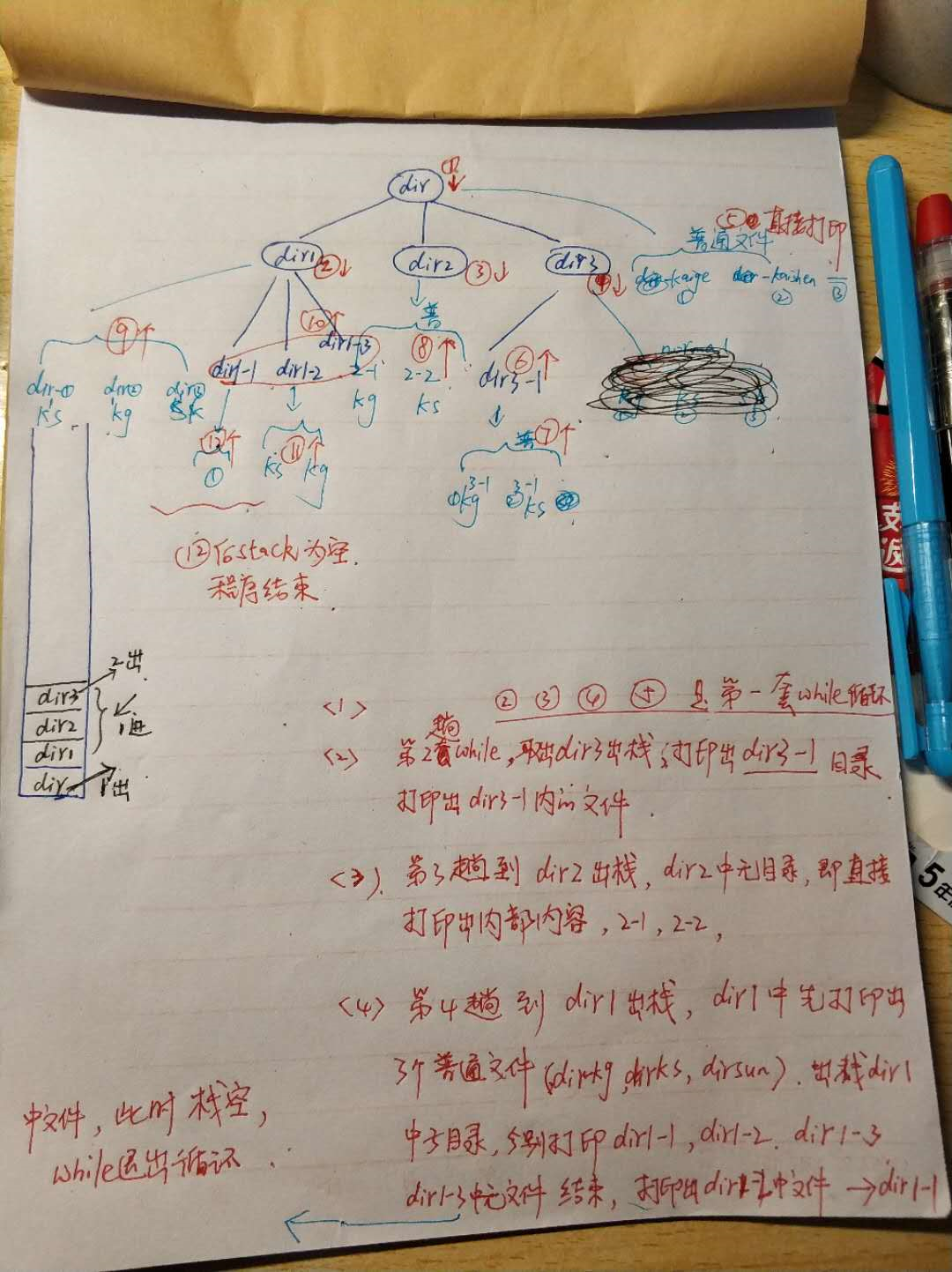

原理分析:

说明:
队列是 先进先出的模型。A先进队,在A出队的时候,C B入队,按图示,C出队,FG 入队,B出队,DE入队,
F出队,JK入队,G出队,无入队,D出队,H I入队,最后E J K H I出队,均无入队了,即每一层一层处理、
故:先进先出的队列结构实现了广度优先遍历。 先进后出的栈结构实现的是深度优先遍历。
代码实现:
其实深度优先和广度优先在代码书写上是差别不大的,基本相同,只是一个是使用栈结构(用列表进行模拟)
另一个(广度优先遍历)是使用了队列的数据结构来达到先进先出的目的。
#__author:"吉**"
#date: 2018/10/21 0021
#function: # 广度优先搜索模拟
# 利用队列来模拟广度优先搜索 import os
import collections def getAllDirIT(path):
queue=collections.deque()
#进队
queue.append(path) #循环,当队列为空,停止循环
while len(queue) != 0:
#出队数据 这里相当于找到A元素的绝对路径
dirPath = queue.popleft()
# 找出跟目录下的所有的子目录信息,或者是跟目录下的文件信息
dirList = os.listdir(dirPath) #遍历该文件夹下的其他信息
for filename in dirList:
#绝对路径
dirAbsPath = os.path.join(dirPath,filename) # 判断:如果是目录dir入队操作,如果不是dir打印出即可
if os.path.isdir(dirAbsPath):
print("目录:"+filename)
queue.append(dirAbsPath)
else:
print("普通文件:"+filename) # 函数的调用
getAllDirIT(r'E:\[AAA](千)全栈学习python\18-10-21\day7\temp\dir')
广度优先运行输出结构:
先图解:按照每一层从左到右遍历即可实现。
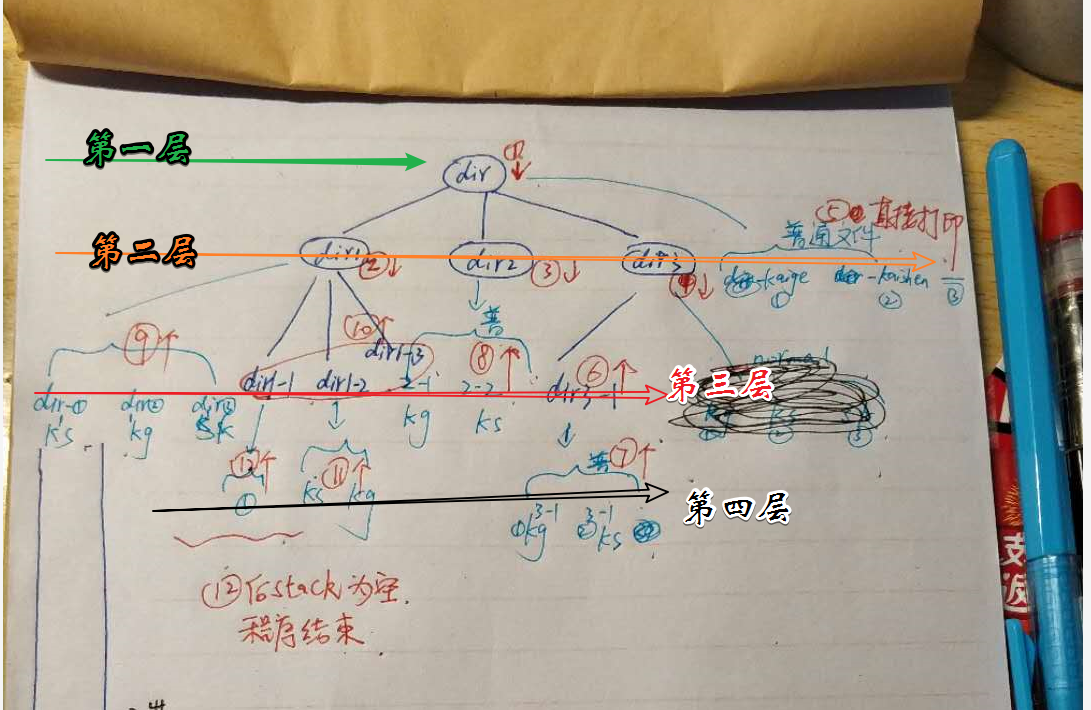

【11】python 递归,深度优先搜索与广度优先搜索算法模拟实现的更多相关文章
- python 递归深度优先搜索与广度优先搜索算法模拟实现
一.递归原理小案例分析 (1)# 概述 递归:即一个函数调用了自身,即实现了递归 凡是循环能做到的事,递归一般都能做到! (2)# 写递归的过程 1.写出临界条件2.找出这一次和上一次关系3.假设当前 ...
- python 递归,深度优先搜索与广度优先搜索算法模拟实现
一.递归原理小案例分析 (1)# 概述 递归:即一个函数调用了自身,即实现了递归 凡是循环能做到的事,递归一般都能做到! (2)# 写递归的过程 1.写出临界条件 2.找出这一次和上一次关系 3.假设 ...
- DFS_BFS(深度优先搜索 和 广度优先搜索)
package com.rao.graph; import java.util.LinkedList; /** * @author Srao * @className BFS_DFS * @date ...
- 【Python排序搜索基本算法】之深度优先搜索、广度优先搜索、拓扑排序、强联通&Kosaraju算法
Graph Search and Connectivity Generic Graph Search Goals 1. find everything findable 2. don't explor ...
- Depth-first search and Breadth-first search 深度优先搜索和广度优先搜索
Depth-first search Depth-first search (DFS) is an algorithm for traversing or searching tree or grap ...
- 递归——深度优先搜索(DFS)——以滑雪问题为例(自顶而下)
一.问题:滑雪 问题描述:小明喜欢滑雪,为了获得速度,滑的区域必须向下倾斜,而且当你滑到坡底,你不得不再次走上坡或者等待升降机来载你.小明想知道在一个区域中最长底滑坡.区域由一个二维数组给出.数组的每 ...
- 11: python递归
1.1 递归讲解 1.定义 1. 在函数内部,可以调用其他函数.如果一个函数在内部调用自身本身,这个函数就是递归函数. 2.递归特性 1. 必须有一个明确的结束条件 2. 每次进入更深一层递归时,问题 ...
- 【js数据结构】图的深度优先搜索与广度优先搜索
图类的构建 function Graph(v) {this.vertices = v;this.edges = 0;this.adj = []; for (var i = 0; i < this ...
- DFS或BFS(深度优先搜索或广度优先搜索遍历无向图)-04-无向图-岛屿数量
给定一个由 '1'(陆地)和 '0'(水)组成的的二维网格,计算岛屿的数量.一个岛被水包围,并且它是通过水平方向或垂直方向上相邻的陆地连接而成的.你可以假设网格的四个边均被水包围. 示例 1: 输入: ...
随机推荐
- C# 装箱与拆箱转换
一.装箱转换(boxing) 装箱时一种隐式转换,它接受值类型的值,根据这个值在堆上创建一个完整的引用类型类型对象并返回对象引用,简单来说就是将值类型转换为引用类型 任何值类型ValueType都可以 ...
- Netty 高性能之道 - Recycler 对象池的复用
前言 我们知道,Java 创建一个实例的消耗是不小的,如果没有使用栈上分配和 TLAB,那么就需要使用 CAS 在堆中创建对象.所以现在很多框架都使用对象池.Netty 也不例外,通过重用对象,能够避 ...
- 微信公众号DOM的一个坑
最近不知道写什么,node的源码有点不知道怎么入手,还在努力学习C++中…… 在写微信公众号的时候遇到了一个小bug,有一个tab栏,在开发者工具.IOS手机上都OK,但是一到我的小米note上就GG ...
- MVC应用程序请求密码的功能(一)
经过一系列的练习,实现了会员注册<MVC会员注册>http://www.cnblogs.com/insus/p/3439599.html,登录<MVC应用程序实现会员登录功能> ...
- LDA算法学习(Matlab实现)
LDA算法 对于两类问题的LDA(Matlab实现) function [ W] = FisherLDA(w1,w2) %W最大特征值对应的特征向量 %w1 第一类样本 %w2 第二类样本 %第一步: ...
- 集合框架(TreeSet原理)
特点: TreeSet是用来排序的,可以指定一个顺序,对象存入之后会按照指定的顺序排列 使用方式: 自然排序(Comparable) TreeSet类的add()方法中会把存入的对象提升为Compar ...
- Java JDBC MySQL
一.驱动 下载地址:https://dev.mysql.com/downloads/connector/j/ 二.数据库连接配置 jdbc:mysql://address:port/database? ...
- 截取URL的某个参数值
原文作者链接 https://www.jianshu.com/p/c9324d237a8e
- 【代码笔记】iOS-获得现在的时间(2015-09-11)
一,代码. - (void)viewDidLoad { [super viewDidLoad]; // Do any additional setup after loading the view, ...
- 全局eslint不生效的处理
react项目里能用上 eslint 的 airbnb 规范真是的,对自己的编码有很好的帮助,不经可以养成良好的代码风格,而且还能检测出 state或者变量 是否 使用过, 然而,所在团队的小伙伴们, ...

