Stable Diffusion扩散模型

人像生成模型

1.模型理论基础

扩散模型（Diffusion Model）：

1.1 Diffusion Model 原理

• 首先，Denoise Model 需要一个起始的噪声图像作为输入。这个噪声图像可以是完全随机的，也可以是一些特定的模式（如 高斯分布）或者形状。 - 接下来，随着 denoise 的不断进行，图像的细节信息会逐渐浮现出来。这个过程有点像冲洗照片，每次冲洗都会逐渐浮现出照片中的细节和色彩。denoise 的次数越多，生成的图像就越清晰、越细腻。 - 最后，Denoise Model 会根据用户的需求输出最终的图像。

Denoise 过程中，用的都是同一个 Denoise Model。为了让 Diffusion Model 知道当前是在哪个 Step 输入的图片，实际操作过程中会把 Step 数字作为输入传递给模型。这样，模型就能够根据当前的 Step 来判断图像的噪声程度，从而进行更加精细的去噪操作。

1.2 Denoise Model 的内部

实际上，Denoise Model 内部做了一些非常有趣的事情来生成高质量的图像。 首先，由于让模型直接预测出去噪后的图片是比较困难的事情，所以 Denoise Model 做了两件事情： - 首先，它会把噪音图片和当前的 Step 一起输入到一个叫做 Noise Predicter 的模块中，这个模块会预测出当前图片的噪音。 - 接下来，模型会对初步的去噪图片进行修正，以达到去噪效果。具体来说，模型会通过像素值减去噪音的方式来进一步去除噪音。

1.3 如何训练 Noise Predictor？

要训练 Noise Predictor，我们需要有 Ground truth 的噪音作为 label 进行有监督的学习。那么，各个 Step 的 Ground truth 从哪里来呢？

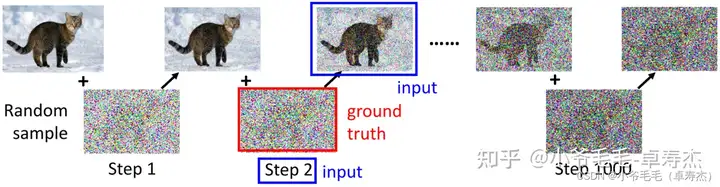
我们可以通过随机产生噪音的方式来模拟扩散过程（Diffusion Process）。具体来说，我们从原始图像开始，不断地加入随机噪音，得到一系列加噪后的图像。这些加噪后的图像和当前的 Step 就是 Denoise Model 的输入，而加入的噪音则是 Ground truth。我们可以用这些 Ground truth 数据来训练 Noise Predictor，以便它能够更好地预测出当前图像的噪音。

1.4 Text-to-Image

有些同学问了：我见到的 Diffusion Model是Text-to-image Generator，基于文本生成图片。为什么你这个没有文本的输入呢？

确实，有些 Diffusion Model 是基于文本生成图片的，这意味着我们可以将文本作为输入来生成图片。

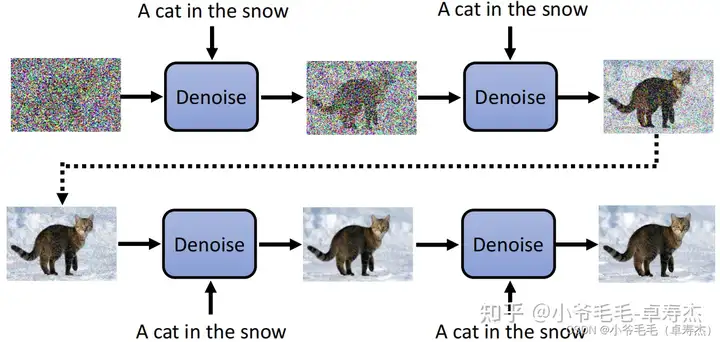
每一个 step，文本都可以作为 Denoise Model 的输入，这样可以让模型知道当前应该生成什么样的图片。

具体来说，我们可以将文本输入到 Noise Predictor 中，以便预测出噪音来去噪。