CNN学习笔记：神经网络表示

CNN学习笔记：神经网络表示

双层神经网络模型

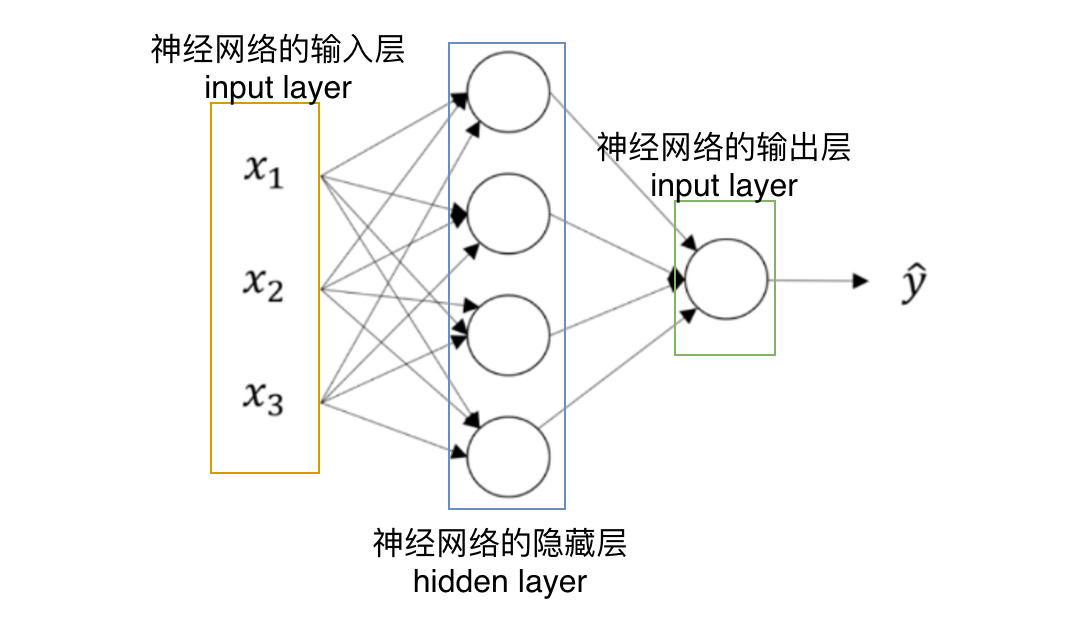
　　在一个神经网络中，当你使用监督学习训练它的时候，训练集包含了输入x还有目标输出y。隐藏层的含义是，在训练集中，这些中间节点的真正数值，我们是不知道的，即在训练集中你看不到他们的数值，我们只能看到输入和输出。

定义神经网络的层数

　　神经网络层数是指，除输入层意外的其他层的合计数，此处只有一层隐藏层和一层输出层。

神经网络的计算过程

　　a^[n]表示第N层神经元的激活函数组成的矩阵，z^[n]函数表示第N层神经元的处理逻辑做出的矩阵，激活函数a通过z函数的数据来产生合理的输出并传递给下一层。

　　

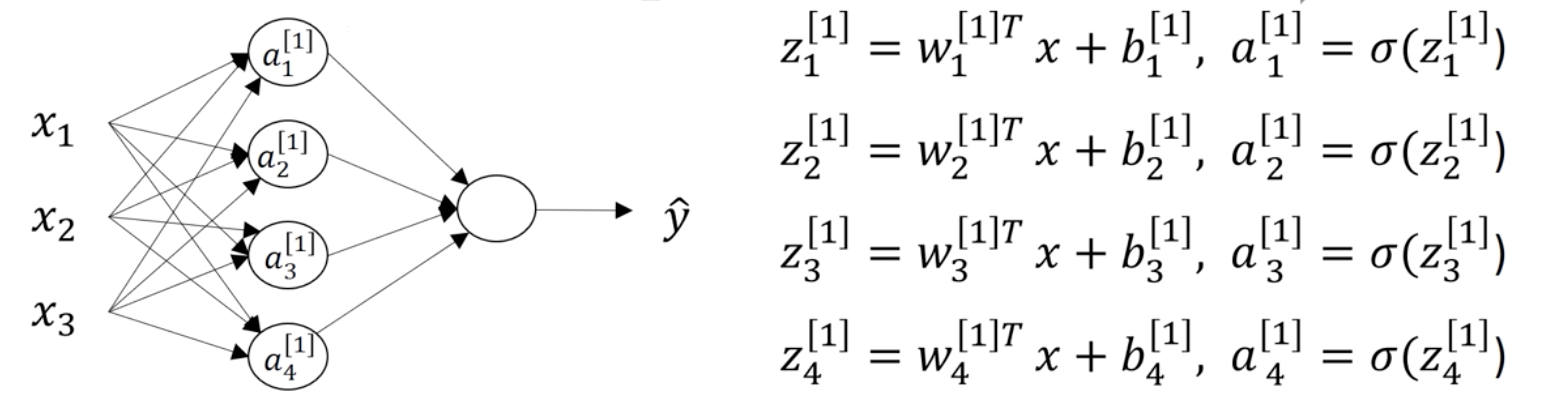
　　如下图所示，Z^[2]的输入来自于上一次激活函数产生的值，是一个四行一列的矩阵，而W[2]是一个一行四列的矩阵，最后运算会产生的a^[2]是一个一行一列的矩阵。

　　 

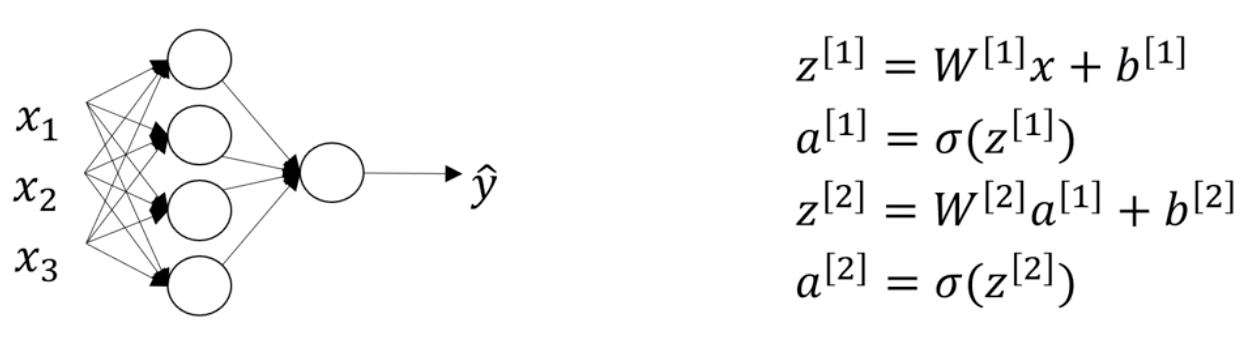
多样本向量化

　　逻辑回归是将各个训练样本组合成矩阵，对矩阵的各列进行计算。神经网络是通过对逻辑回归中的等式简单的变形，让神经网络计算出输出值。这种计算是所有的训练样本同时进行的。

　　如果我们有多个输入样例，我们可以使用传统的for语句实现，但是它依旧是线性运算，我们没有利用到计算机高效的矩阵运算能力。

　　

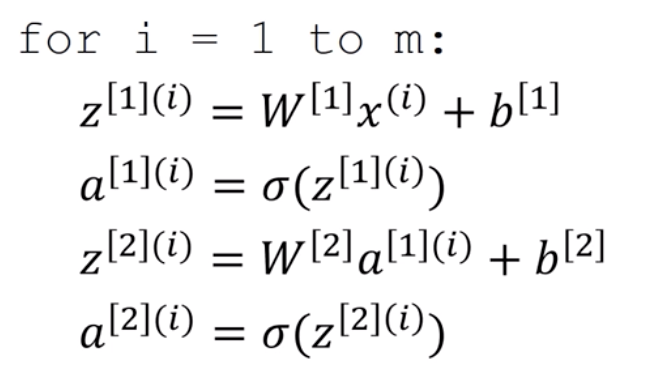
　　我们可以将其向量化如下，其中（i）表示第i个样本

　　

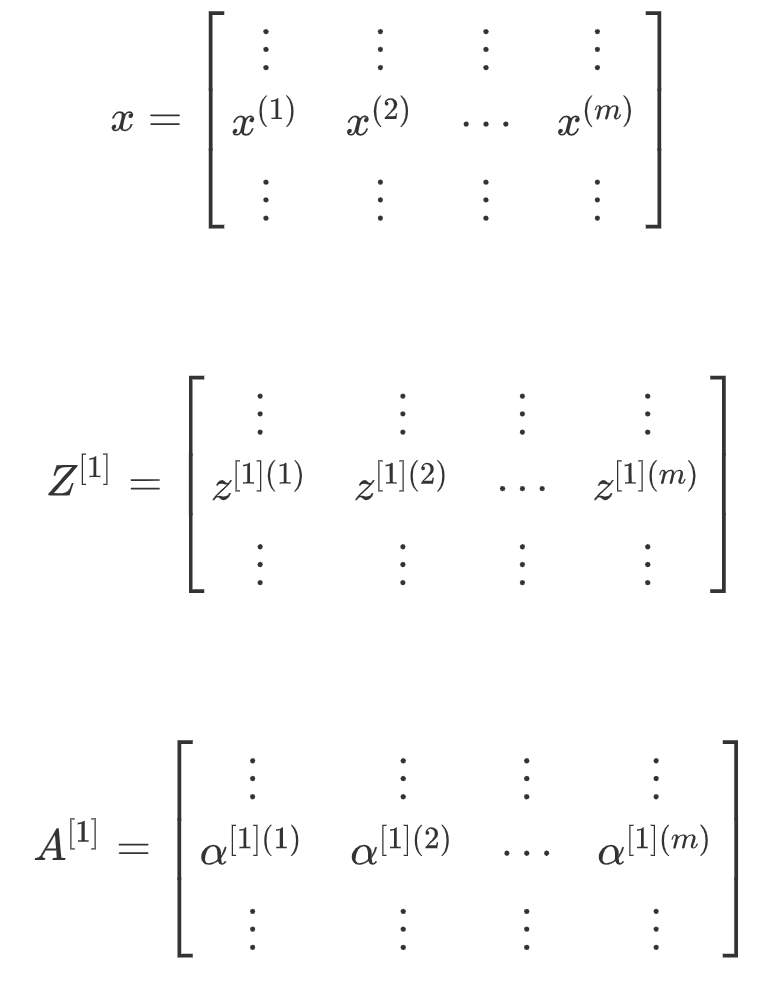
　　这样，我们将多个样本向量化运算过程整理如下

　　

　　这种符号其中一个作用就是，可以通过训练样本来进行索引。这就是水平索引对应于不同的训练样本的原因，这些训练样本是从左到右扫描训练集而得到的。

　　在垂直方向，这个垂直索引对应于神经网络中的不同节点。例如，位于矩阵的最左上角对应于激活单元，它是位于第一个训练样本上的第一个隐藏单元。它的下一个值对应于第二个隐藏单元的激活值。它是位于第一个训练样本上的，以及第一个训练示例中第三个隐藏单元，等等。

　　当垂直扫描，是索引到隐藏单位的数字。当水平扫描，将从第一个训练示例中从第一个隐藏的单元到第二个训练样本，第三个训练样本……直到节点对应于第一个隐藏单元的激活值，且这个隐藏单元是位于这个训练样本中的最终训练样本。

　　从水平上看，矩阵代表了各个训练样本。从竖直上看，矩阵的不同的索引对应于不同的隐藏单元。

　　对于矩阵，情况也类似，水平方向上，对应于不同的训练样本；竖直方向上，对应不同的输入特征，而这就是神经网络输入层中各个节点。