1.4 正则化 regularization

　　如果你怀疑神经网络过度拟合的数据，即存在高方差的问题，那么最先想到的方法可能是正则化，另一个解决高方差的方法就是准备更多数据，但是你可能无法时时准备足够多的训练数据，或者获取更多数据的代价很高。但正则化通常有助于避免过拟合或者减少网络误差，下面介绍正则化的作用原理。

我们用逻辑回归来实现这些设想。

逻辑回归的损失函数为

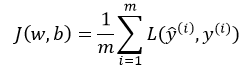
　　然后求损失函数J的最小值

　　其中，分别表示预测值与真实值，w,b是逻辑回归的两个参数，。

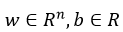　　在逻辑回归中加入正则化，只需要添加参数λ，也就是正则化参数，式子如下：

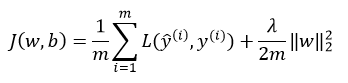
　　其中，向量参数w的欧几里得（L2）范数平方为：

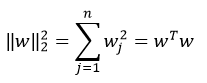
以上方法称为L2正则化。

　　为什么只有正则化参数w，而不加上参数b呢？其实，也可以加上，但是一般情况下可以省略不写，因为w通常是一个高维的参数矢量，已经可以表达高偏差问题，w可能含有很多参数，我们不可能拟合所以参数，而b只是单个数字，所以w几乎涵盖所有参数，而不是b。如果加了参数b，其实也没什么太大影响，因为b只是众多参数中的一个。

　　L2正则化是最常见的正则化类型，你们可能听说过L1正则化，L1正则项如下：

　　如果用的是L1正则化，w最终会是稀疏的，也就是说w向量中有很多0，有人时这样有利于压缩模型，因为集合中参数均为0，存储该模型所占的内存更少。实际上，虽然L1正则化使得模型变得稀疏，却没有降低太多存储内存，所以Angrew NG认为这并不是L1正则化的目的，至少不是为了压缩模型。人们在训练神经网络时，越来越倾向于使用L2正则化。

　　最后一个细节，λ是正则化参数，我们通常使用验证集或者交叉验证来配置这个参数，尝试寻找各种各样的数据，寻找最好的参数，我们要考虑训练集之间的权衡，把参数正常值设置为较小值，这样可以避免过拟合。因此λ是另外一个需要调整的超参数。顺便说一下，为了方便编写代码，在Python中，lambda是一个保留关键字。

　　以上就是在逻辑回归函数中实现L2正则化的过程。

-----------------------------------------------------------------

　　如何在神经网络中实现呢？

　　神经网络中损失函数如下：

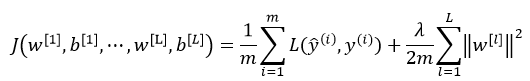
　　其中，L表示神经网络的层数，w是一个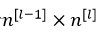的多维矩阵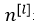，表示第l层神经元个数。

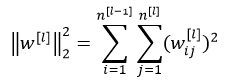
　　该矩阵范数被称为“弗罗贝尼乌斯范数（Frobenius norm）”，（矩阵中不称为L2范数），表示一个矩阵中所有元素的平方和。

　　如何使用该范数实现梯度下降呢？

　　用backprop计算出dw，backprop会给出j对w的偏导数，方法如下图：

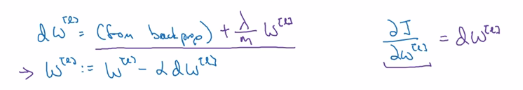
　　由上面可知，L2正则化有时被称为权重衰减（weight decay）

　　即，不加L2正则项时，的更新方式为：

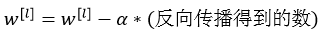
加上L2正则项之后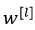，的更新方式变为：

该正则项说明，不论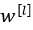是什么，我们都试图让它变得更小，实际上，相当于我们给矩阵W乘以了倍的权重，该倍数小于1，因此L2正则化也被称为权重衰减（weight decay）。

以上就是神经网络中实现L2正则化的过程。

为什么正则化可以预防过拟合？请看下一节。