IO模型（epoll）--详解-03

写在前面

　　epoll是开发linux高性能服务器的必备技术至，epoll本质，是服务端程序员的必须掌握的知识。

七、epoll的原理和流程

　　本节会以示例和图表来讲解epoll的原理和流程。

创建epoll对象

　　如下图所示，当某个进程调用epoll_create方法时，内核会创建一个eventpoll对象（也就是程序中epfd所代表的对象）。eventpoll对象也是文件系统中的一员，和socket一样，它也会有等待队列。内核创建eventpoll对象

　　创建一个代表该epoll的eventpoll对象是必须的，因为内核要维护“就绪列表”等数据，“就绪列表”可以作为eventpoll的成员。

维护监视列表

　　创建epoll对象后，可以用epoll_ctl添加或删除所要监听的socket。以添加socket为例，如下图，如果通过epoll_ctl添加sock1、sock2和sock3的监视，内核会将eventpoll添加到这三个socket的等待队列中。添加所要监听的socket

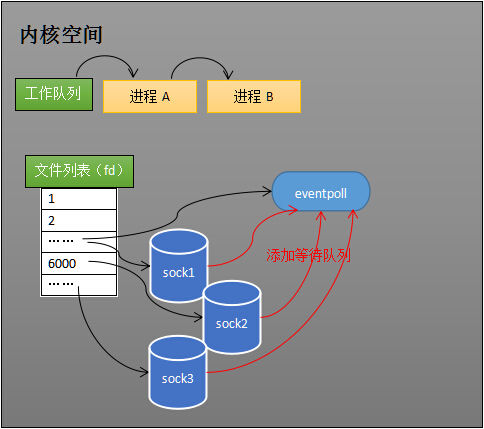
　　当socket收到数据后，中断程序会操作eventpoll对象，而不是直接操作进程。

接收数据

　　当socket收到数据后，中断程序会给eventpoll的“就绪列表”添加socket引用。如下图展示的是sock2和sock3收到数据后，中断程序让rdlist引用这两个socket。给就绪列表添加引用

　　

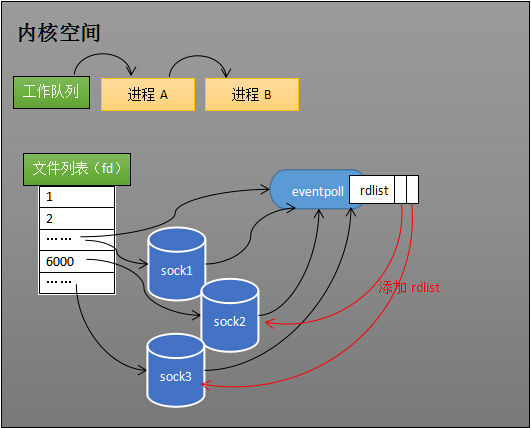
　　eventpoll对象相当于是socket和进程之间的中介，socket的数据接收并不直接影响进程，而是通过改变eventpoll的就绪列表来改变进程状态。

　　当程序执行到epoll_wait时，如果rdlist已经引用了socket，那么epoll_wait直接返回，如果rdlist为空，阻塞进程。

阻塞和唤醒进程

　　假设计算机中正在运行进程A和进程B，在某时刻进程A运行到了epoll_wait语句。如下图所示，内核会将进程A放入eventpoll的等待队列中，阻塞进程。epoll_wait阻塞进程

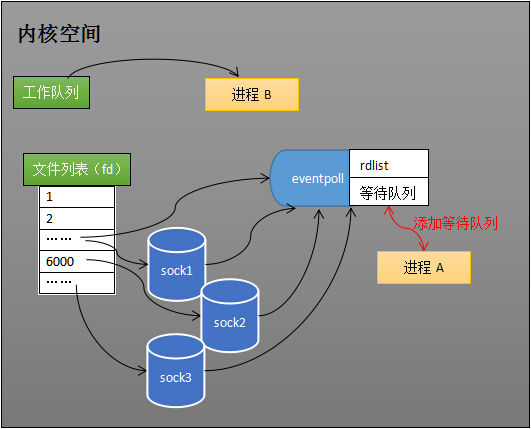
　　当socket接收到数据，中断程序一方面修改rdlist，另一方面唤醒eventpoll等待队列中的进程，进程A再次进入运行状态（如下图）。也因为rdlist的存在，进程A可以知道哪些socket发生了变化。epoll唤醒进程

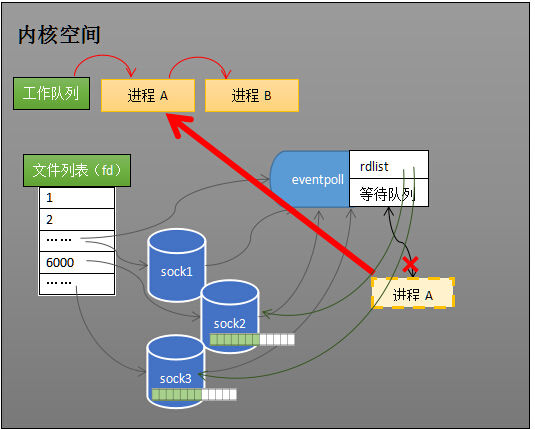
八、epoll的实现细节

至此，相信读者对epoll的本质已经有一定的了解。但我们还留有一个问题，eventpoll的数据结构是什么样子？

再留两个问题，就绪队列应该应使用什么数据结构？eventpoll应使用什么数据结构来管理通过epoll_ctl添加或删除的socket？

如下图所示，eventpoll包含了lock、mtx、wq（等待队列）、rdlist等成员。rdlist和rbr是我们所关心的。

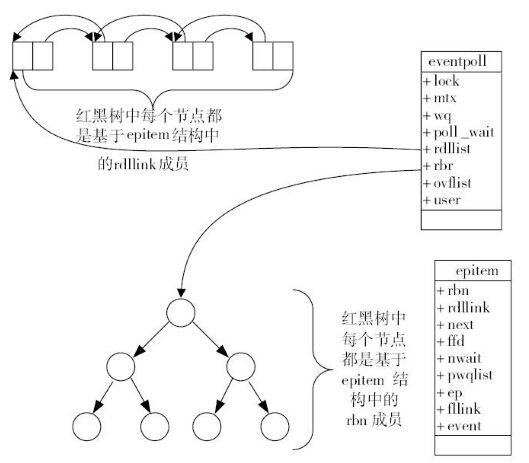
就绪列表的数据结构

　　就绪列表引用着就绪的socket，所以它应能够快速的插入数据。

　　程序可能随时调用epoll_ctl添加监视socket，也可能随时删除。当删除时，若该socket已经存放在就绪列表中，它也应该被移除。

　　所以就绪列表应是一种能够快速插入和删除的数据结构。双向链表就是这样一种数据结构，epoll使用双向链表来实现就绪队列（对应上图的rdllist）。

索引结构

　　既然epoll将“维护监视队列”和“进程阻塞”分离，也意味着需要有个数据结构来保存监视的socket。至少要方便的添加和移除，还要便于搜索，以避免重复添加。红黑树是一种自平衡二叉查找树，搜索、插入和删除时间复杂度都是O(log(N))，效率较好。epoll使用了红黑树作为索引结构（对应上图的rbr）。

ps：因为操作系统要兼顾多种功能，以及由更多需要保存的数据，rdlist并非直接引用socket，而是通过epitem间接引用，红黑树的节点也是epitem对象。同样，文件系统也并非直接引用着socket。为方便理解，本文中省略了一些间接结构。

九、结论

epoll在select和poll（poll和select基本一样，有少量改进）的基础引入了eventpoll作为中间层，使用了先进的数据结构，是一种高效的多路复用技术。

再留一点作业！

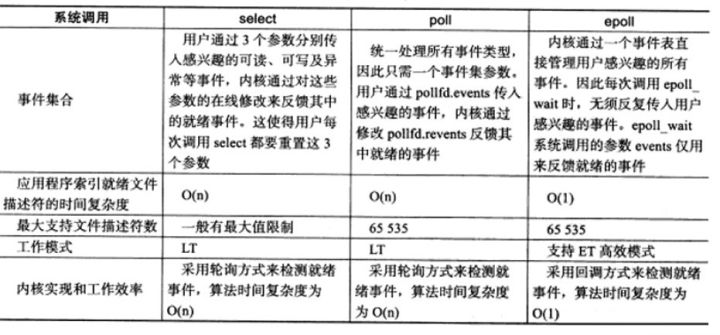
下表是个很常见的表，描述了select、poll和epoll的区别。读完本文，读者能否解释select和epoll的时间复杂度为什么是O(n)和O(1)？