Codeforces Round #384 (Div. 2) C. Vladik and fractions（构造题）

传送门

Description

Vladik and Chloe decided to determine who of them is better at math. Vladik claimed that for any positive integer n he can represent fraction   as a sum of three distinct positive fractions in form .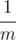

Help Vladik with that, i.e for a given n find three distinct positive integers x, y and z such that  . Because Chloe can't check Vladik's answer if the numbers are large, he asks you to print numbers not exceeding 10⁹.

If there is no such answer, print -1.

Input

The single line contains single integer n (1 ≤ n ≤ 10⁴).

Output

If the answer exists, print 3 distinct numbers x, y and z (1 ≤ x, y, z ≤ 10⁹, x ≠ y, x ≠ z, y ≠ z). Otherwise print -1.

If there are multiple answers, print any of them.

Sample Input

3

7

Sample Output

2 7 42

7 8 56

思路

题意：

给出一个数 n ，问是否存在三个不同的整数 x ,y ,z 满足。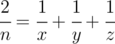

题解:

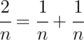，因此，我们可以让1/z = 1 / n，剩下的为 1/x + 1/y = 1/n，通过恒等变换可以知道 1/x = ny / (y - n)，可以发现，y = n + 1时候，x 必然为整数，因此x = n  + n * n，y = n + 1，z = n。需要注意的是，当 n = 1时，x = 2，y = 2，不符合题意。

#include<bits/stdc++.h>
using namespace std;

int main()
{
	int n;
	scanf("%d",&n);
	if (n == 1)	printf("-1\n");
	else	printf("%d %d %d\n",n*n + n,n + 1,n);
	return 0;
}