hdu1045 - 贪心，二分图

题目链接

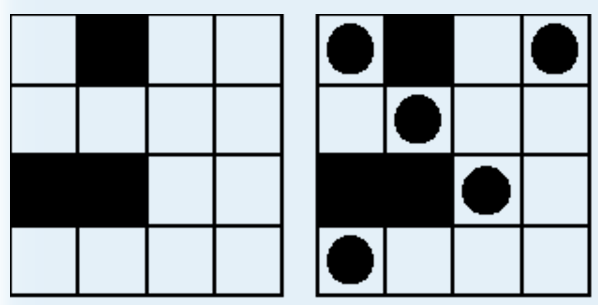
左边白方格里放小球，满足同一行、列只有一个(被黑块隔开)。问最多放多少个球。

------------------------------------------------------------------------------------------------------------

从贪心类别看到这个题的，读完题后只能想到枚举的解法 ==。智商有限。

看了题解后才知道怎么贪心，还有一个最大二分匹配的解法。

1.枚举

依次判断每个格子能不能放小球，如果能则返回 max{dfs(放)，dfs(不放)}，否则返回dfs(不放).

#define _CRT_SECURE_NO_DEPRECATE
#include <set>
#include <map>
#include <stack>
#include <queue>
#include <cmath>
#include <vector>
#include <string>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>

#define MAX(a,b) ((a)>=(b)?(a):(b))
#define MIN(a,b) ((a)<=(b)?(a):(b))
#define OO 0x0fffffff
typedef long long LL;
using namespace std;
typedef pair<int, int> int2;
const int dir[][] = { { ,  }, { -,  }, { ,  }, { , - } };
char status[][];
int2 dots[];
int dotcnt;
int n;

int dfs(int depth){
    if (depth == dotcnt){
        int ret = ;
        for (int i = ; i<n; i++) for (int j = ; j<n; j++) if (status[i][j] == '*') ret++;
        return ret;
    }
    int x = dots[depth].first;
    int y = dots[depth].second;
    bool flag = true;

    for (int i = ; i<; i++){
        for (int j = ; flag; j++){
            int tx = x + dir[i][] * j;
            int ty = y + dir[i][] * j;
            if (tx< || ty< || tx >= n || ty >= n) break;
            if (status[tx][ty] == 'X') break;
            if (status[tx][ty] == '*') { flag = false; break; }
        }
    }
    int no = dfs(depth + );
    if (flag) {
        status[x][y] = '*';
        int yes = dfs(depth + );
        status[x][y] = '.';
        return max(no,yes);
    }
    else return no;
}

int main(){
    while (scanf("%d", &n), n){
        dotcnt = ;
        for (int i = ; i<n; i++) {
            scanf("%s", status[i]);
            for (int j = ; j<n; j++)
                 if (status[i][j] != 'X') dots[dotcnt++] = make_pair(i, j);
        }
        printf("%d\n", dfs());
    }
    return ;
}

2. 贪心

统计每个白块所在行和列的连通区域的面积s，从第一排开始处理，找到s最小的块，标记，继续找第一排中最小的，如果没有了则挪到下一排。

3. 二分匹配

现在还没复习到二分图，只写一下二分图的构造：

a. 列收缩。所有列中每一个联通的白块看做一个点。记该序列为A;

b. 行收缩。得到序列B;

c. 连边。对所有(a,b)属于（A,B）,如果ab相交则连一条边

接下来就是最大二分匹配了