BZOJ 4289: PA2012 Tax(最短路)

Time Limit: 10 Sec Memory Limit: 128 MB
Submit: 755 Solved: 240
[Submit][Status][Discuss]

Description

给出一个N个点M条边的无向图，经过一个点的代价是进入和离开这个点的两条边的边权的较大值，求从起点1到点N的最小代价。起点的代价是离开起点的边的边权，终点的代价是进入终点的边的边权

N<=100000

M<=200000

Input

Output

Sample Input

4 5
1 2 5
1 3 2
2 3 1
2 4 4
3 4 8

Sample Output

HINT

Source

这题居然卡long long，也是没谁了

首先一个很显然的思路是暴力拆边

即把每个点每一条入边和每一条出边的两两看做一个点，权值为两边的较大值

但是这样很显然是$O(m^2)$，肯定会GG

所以我们考虑一种神仙操作。

对于一条无向边，我们把它看成两条有向边

然后我们这样构图

1.对于一个点，我们把它的出边从小到大排序

2.枚举每一条边，如果这条边连接着1或者N，那么我们从S连向这条边或者从这条边连向T，权值为该边的权值

3.从改边所对应的入边向该边连一条边，边权为它们的权值

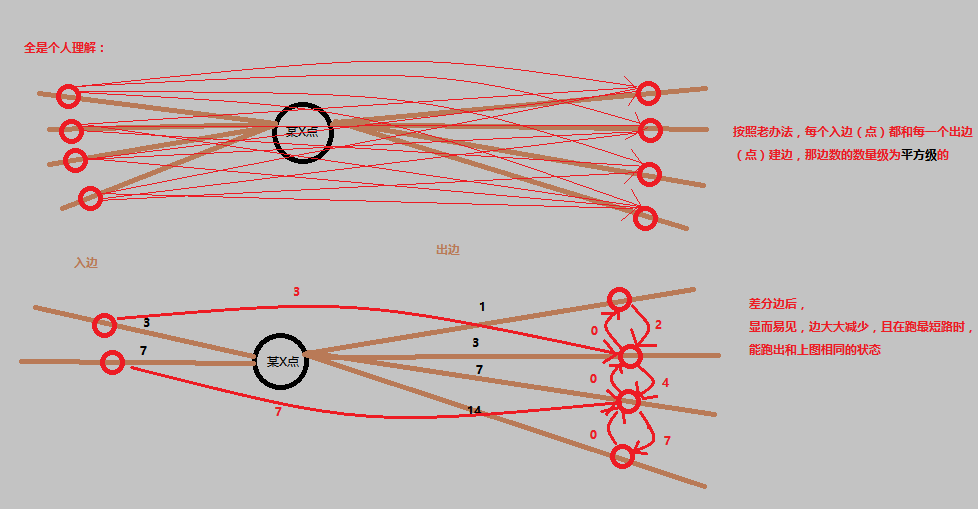
4.枚举每一条出边，从权值较小的向权值较大的连权值为两边差值的边，从权值较大的向权值较小的连权值为0的边

可能这样说不是很清楚，借鉴一下这位大佬的图

#include<cstdio>

#include<algorithm>

#include<queue>

#include<cstring>

#define Pair pair<long long,int>

#define F first

#define S second

const int MAXN=*1e6+;

using namespace std;

inline int read()

{

    char c=getchar();int x=,f=;

    while(c<''||c>''){if(c=='-')f=-;c=getchar();}

    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}

    return x*f;

}

struct Edge

{

    int u,v,w,nxt;

}E[MAXN];

int headE[MAXN],numE=;

inline void add_edge(int x,int y,int z)

{

    E[numE].u=x;

    E[numE].v=y;

    E[numE].w=z;

    E[numE].nxt=headE[x];

    headE[x]=numE++;

}

struct node

{

    int u,v,w,nxt;

}edge[MAXN];

int head[MAXN],num=;

inline void AddEdge(int x,int y,int z)

{

    edge[num].u=x;

    edge[num].v=y;

    edge[num].w=z;

    edge[num].nxt=head[x];

    head[x]=num++;

}

int N,M,S,T;

int temp[MAXN];

long long  dis[MAXN];

bool vis[MAXN];

void Dijstra()

{

    memset(dis,0xf,sizeof(dis));dis[S]=;

    priority_queue<Pair>q;

    q.push(make_pair(,S));

    while(q.size()!=)

    {

        while(vis[q.top().second]&&q.size()>) q.pop();

        long long  p=q.top().second;

        vis[p]=;

        for(int i=head[p];i!=-;i=edge[i].nxt)

            if(dis[edge[i].v]>dis[p]+edge[i].w)

                dis[edge[i].v]=dis[p]+edge[i].w,

                q.push(make_pair(-dis[edge[i].v],edge[i].v));

    }

    printf("%lld\n",dis[T]);

}

int comp(const int &a,const int &b)

{

    return E[a].w<E[b].w;

}

int main()

{

    #ifdef WIN32

    freopen("a.in","r",stdin);

    #else

    #endif

    memset(headE,-,sizeof(headE));

    memset(head,-,sizeof(head));

    N=read();M=read();S=,T=*(M+);

    for(int i=;i<=M;i++)

    {

        int x=read(),y=read(),z=read();

        add_edge(x,y,z);

        add_edge(y,x,z);

    }

    for(int i=;i<=N;i++)

    {

        int tempnum=;

        for(int j=headE[i];j!=-;j=E[j].nxt)

            temp[++tempnum]=j;

        sort(temp+,temp+tempnum+,comp);

        for(int j=;j<=tempnum;j++)

        {

            int x=temp[j],y=temp[j+];

            if(E[x].u==)

                AddEdge(S,x,E[x].w);

            if(E[x].v==N)

                AddEdge(x,T,E[x].w);

            AddEdge(x^,x,E[x].w);

            if(j!=tempnum)

                AddEdge(x,y,E[y].w-E[x].w),

                AddEdge(y,x,);

        }

    }

    Dijstra();

    return ;

}