poj1330 lca 最近公共祖先问题学习笔记

首先推荐两个博客网址：

http://dongxicheng.org/structure/lca-rmq/

http://scturtle.is-programmer.com/posts/30055.html

[转]tarjan算法的步骤是(当dfs到节点u时):
1 在并查集中建立仅有u的集合,设置该集合的祖先为u
1 对u的每个孩子v:
   1.1 tarjan之
   1.2 合并v到父节点u的集合,确保集合的祖先是u
2 设置u为已遍历
3 处理关于u的查询,若查询(u,v)中的v已遍历过,则LCA(u,v)=v所在的集合的祖先
 
举例说明(非证明):

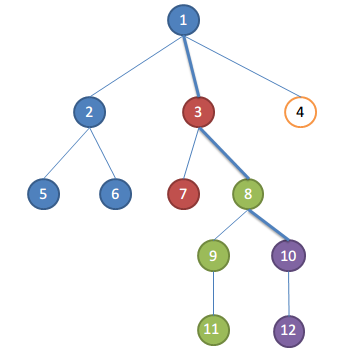
假设遍历完10的孩子,要处理关于10的请求了
取根节点到当前正在遍历的节点的路径为关键路径,即1-3-8-10
集合的祖先便是关键路径上距离集合最近的点
比如此时:
    1,2,5,6为一个集合,祖先为1,集合中点和10的LCA为1
    3,7为一个集合,祖先为3,集合中点和10的LCA为3
    8,9,11为一个集合,祖先为8,集合中点和10的LCA为8
    10,12为一个集合,祖先为10,集合中点和10的LCA为10
你看,集合的祖先便是LCA吧,所以第3步是正确的
道理很简单,LCA(u,v)便是根至u的路径上到节点v最近的点

为什么要用祖先而且每次合并集合后都要确保集合的祖先正确呢?
因为集合是用并查集实现的,为了提高速度,当然要平衡加路径压缩了,所以合并后谁是根就不确定了,所以要始终保持集合的根的祖先是正确的
关于查询和遍历孩子的顺序:
wikipedia上就是上文中的顺序,很多人的代码也是这个顺序
但是网上的很多讲解却是查询在前,遍历孩子在后,对比上文,会不会漏掉u和u的子孙之间的查询呢?
不会的
如果在刚dfs到u的时候就设置u为visited的话,本该回溯到u时解决的那些查询,在遍历孩子时就会解决掉了
这个顺序问题就是导致我头大看了很久这个算法的原因,也是絮絮叨叨写了本文的原因,希望没有理解错= =

对于这道题

题意：求最近公共祖先lca

下面是学来的tarjan代码

 #include <iostream>
 #include <algorithm>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <cmath>
 #include <ctime>

 using namespace std;

 class Edge
 {
     public:
     int    to;
     int    next;
 }e[];

 int    n,T,cnt;
 int    f[],depth[],anc[],p[];
 bool    visited[],In[];

 inline    void    Add_edge(const int & x,const int & y)
 {
     e[++cnt].to=y;
     e[cnt].next=p[x];
     p[x]=cnt;
     return ;
 }

 inline    int    get_anc(const int &x)
 {
     return f[x]==x ? x:f[x]=get_anc(f[x]);
 }

 inline    void    Union(const int & x,const int & y)
 {
     int    S,T;
     S=get_anc(x);
     T=get_anc(y);
     if(S==T)return ;
     if(depth[S]<=depth[T])
         f[S]=T,depth[S]+=depth[T];
     else
         f[T]=S,depth[T]+=depth[S];
     return ;
 }

 void    Dfs(const int &S,const int d)
 {
     int    i;
     depth[S]=d;
     for(i=p[S];i;i=e[i].next)
     {
         Dfs(e[i].to,d+);
     }

     return ;
 }

 int    Lca_tarjan(const int & s,const int & t,const int & u)
 {
     int    i,temp;

     anc[u]=u;
     for(i=p[u];i;i=e[i].next)
     {
         temp=Lca_tarjan(s,t,e[i].to);
         if(temp)return temp;
         Union(u,e[i].to);
         anc[get_anc(u)]=u;
     }

     visited[u]=true;
     if(s==u&&visited[t])
         return anc[get_anc(t)];
     if(t==u&&visited[s])
         return anc[get_anc(s)];

     return ;
 }

 inline    void    Init()
 {
     cnt=;
     memset(depth,,sizeof(depth));
     memset(visited,,sizeof(visited));
     memset(anc,,sizeof(anc));
     memset(p,,sizeof(p));
     memset(e,,sizeof(e));
     memset(In,,sizeof(In));

     for(int i=;i<=n;++i)
     {
         f[i]=i;
     }

     return ;
 }

 int main()
 {
     //freopen("1330.in","r",stdin);

     int    i,x,y,s,t,S;

     scanf("%d",&T);
     while(T--)
     {
         scanf("%d",&n);
         Init();
         for(i=;i<n;++i)
         {
             scanf("%d%d",&x,&y);
             Add_edge(x,y);
             In[y]=true;
         }

         for(S=;S<=n;++S)
             if(!In[S])break;

         scanf("%d%d",&s,&t);
         Dfs(S,);
         printf("%d\n",Lca_tarjan(s,t,S));
     }

     return ;
 }