【十天自制软渲染器】DAY 02：画一条直线（DDA 算法 & Bresenham’s 算法）

推荐关注公众号「卤蛋实验室」或访问博客原文，更新更及时，阅读体验更佳

第一天我们搭建了 C++ 的运行环境并画了一个点，根据 点 → 线 → 面 的顺序，今天我们讲讲如何画一条直线。

本文主要讲解直线绘制算法的推导和思路（莫担心，只涉及到一点点的中学数学知识），最后会给出代码实现，大家放心的看下去就好。

1.DDA 直线算法

1.1 简单实现

我们先来回顾一下中学的几何知识，如何在二维平面内表示一条直线？最常见的就是斜截式了：

其中斜率是，直线在轴上的截距是。

斜截式在数学上是没啥问题的，但是在实际的工程项目中，因为硬件资源是有限的，我们不可能也没必要表示一条无限长度的直线，现实往往是已知一条线段的起点和终点 )，然后把它画出来。

这时候用两点式表示一根直线是最方便的，其中，：

把上面的式子稍作变形，可以把和用参数表示：

这时候我们只要取不同的，就可以得出对应的 x 和 y。

按照以上的思路，我们可以用代码实现一下。C++ 的实现也很简单，如下所示（dl 表示）：

void line(
  int x1, int y1, 
  int x2, int y2, 
  TGAImage &image, TGAColor color) { 
    const float dl = 0.01;
    int dx = x2 - x1;
    int dy = y2 - y1;
    for (float t=0.0; t<1.0; t+=dl) { 
        int x = x1 + dx * t;
        int y = y1 + dy * t;
        image.set(x, y, color);
    } 
}

这个是直线算法的初步实现，只能说「能用」，地位和排序算法里的「冒泡排序」一样，目的达到了，但是性能不太好：

每画一个点，都要运行两次乘法
大量使用浮点运算（众所周知， < < ）
如果 dl 取的比较小，会导致一个像素点会被绘制多次，重复计算
如果 dl 取的比较大，会导致直线断掉

1.2 优化

下面我们就一步一步优化上面的算法。

首先我们注意到，对于屏幕绘制直线这个场景，理论上是连续的，但实际是离散的。

比如说从变化到时，每次绘制时，都是按步长 1 增长的，也就是。

这时候。

我们把上面的公式写成代码，就是下面这个样子：

void line(
  int x1, int y1, 
  int x2, int y2, 
  TGAImage &image, TGAColor color) { 
  float x = x1;
  float y = y1;
  float step = std::abs(x2 - x1);
  float dlx = (x2 - x1) / step;
  float dly = (y2 - y1) / step;
  
  for (int i=1; i<step; i++) { 
    image.set(x, y, color);
    x = x + dlx;
    y = y + dlx;
  } 
}

这个算法其实还有一点儿问题，就是绘制斜率大于 1 的直线时，绘制出的直线会断掉。比如说从 (0, 0) 点绘制到 (2, 4) 点，按照上面的算法只会绘制两个点，但是我们期望的是右图那样，起码各个像素要连接起来：

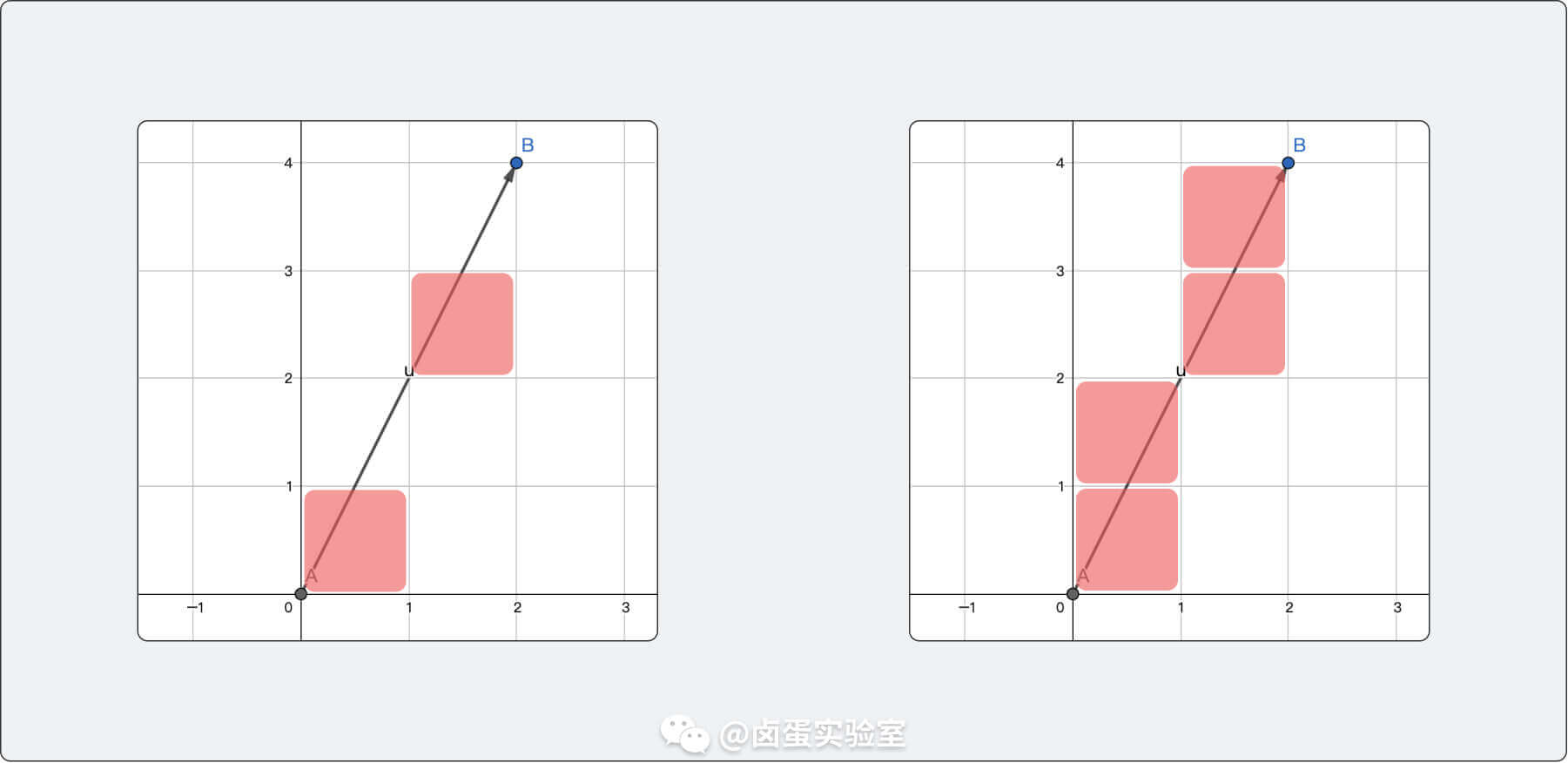
解决方法也很简单，绘制这种比较「陡峭」的直线时（斜率绝对值大于 1），以 y 的变化为基准，而不是以 x，这样就可以避免上面直线不连续情况。

最后的直线算法就是这样：

void line(
  int x1, int y1, 
  int x2, int y2, 
  TGAImage &image, TGAColor color) { 
  float x = x1;
  float y = y1;
  int dx = x2 - x1;
  int dy = y2 - y1;
  float step;
  float dlx, dly;

  // 根据 dx 和 dy 的长度决定基准
  if (std::abs(dx) >= std::abs(dy)) {
    step = std::abs(dx);
  } else {
    step = std::abs(dy);
  }

  dlx = dx / step;
  dly = dy / step;

  for (int i=1; i<step; i++) {
    image.set(x, y, color);
    x = x + dlx;
    y = y + dly;
  }
}

然后我们用这个算法测试一下不同起点不同斜率的直线，看效果运行良好：

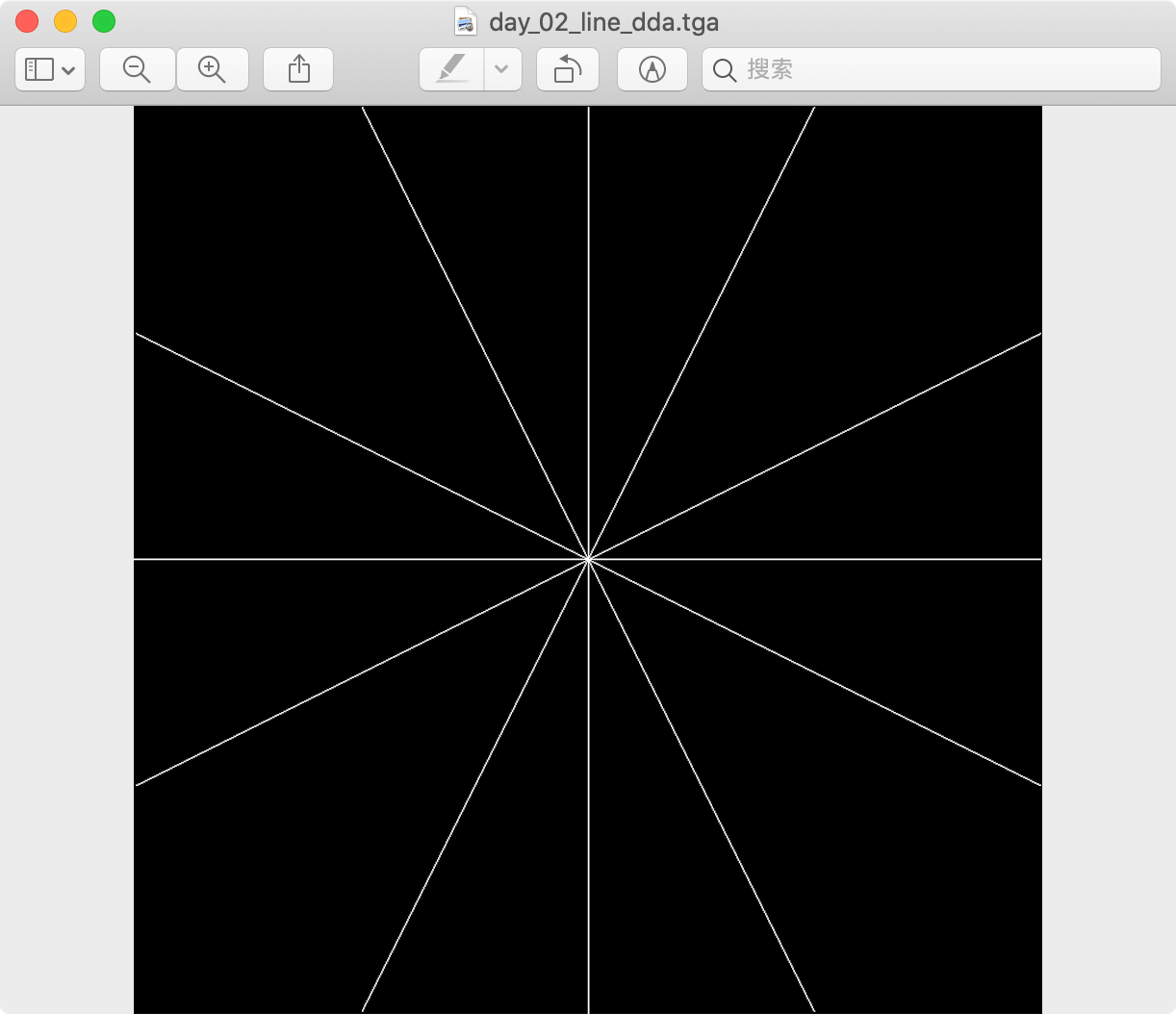
这个算法就是经典的 DDA (Digital differential analyzer) 算法，他比我们一开始的代码要高效的多：

消除了循环内的乘法运算
避免了重复的绘制运算
保证线段连续不会断掉

但是它还有个很耗性能的问题：计算过程中涉及大量的浮点运算。

作为渲染器最底层的算法，我们肯定希望是越快越好。下面我们就来学习一下，消除浮点运算的 Bresenham’s 直线算法。

2.Bresenham’s 直线算法

2.1 初步实现

本节内容不会从一开始就讲完善版的 Bresenham’s 算法，我们先从一个小节开始推导，最后推导出完善的算法。

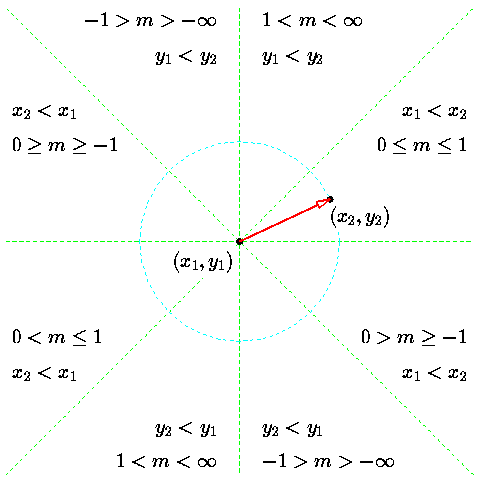
最一开始，我们先考虑所有直线里的一个子集，即斜率范围在之间的直线：。

上一小节里我们说过，对于屏幕绘制直线这个场景，理论上是连续的，但实际是离散的。我们先假设已经绘制了一个点，那么在像素屏幕上，下一个新点的位置，只可能有两种情况：

那么问题就转化为，下一个新点的位置该如何选择？

我想大家应该都想到方案了，大体思路如下

先把这个值带入直线方程里，算出来的值
然后比较和的大小
- ，选点
- ，选点

我们再把思路完善一下，把每次取舍时的误差考虑进去：

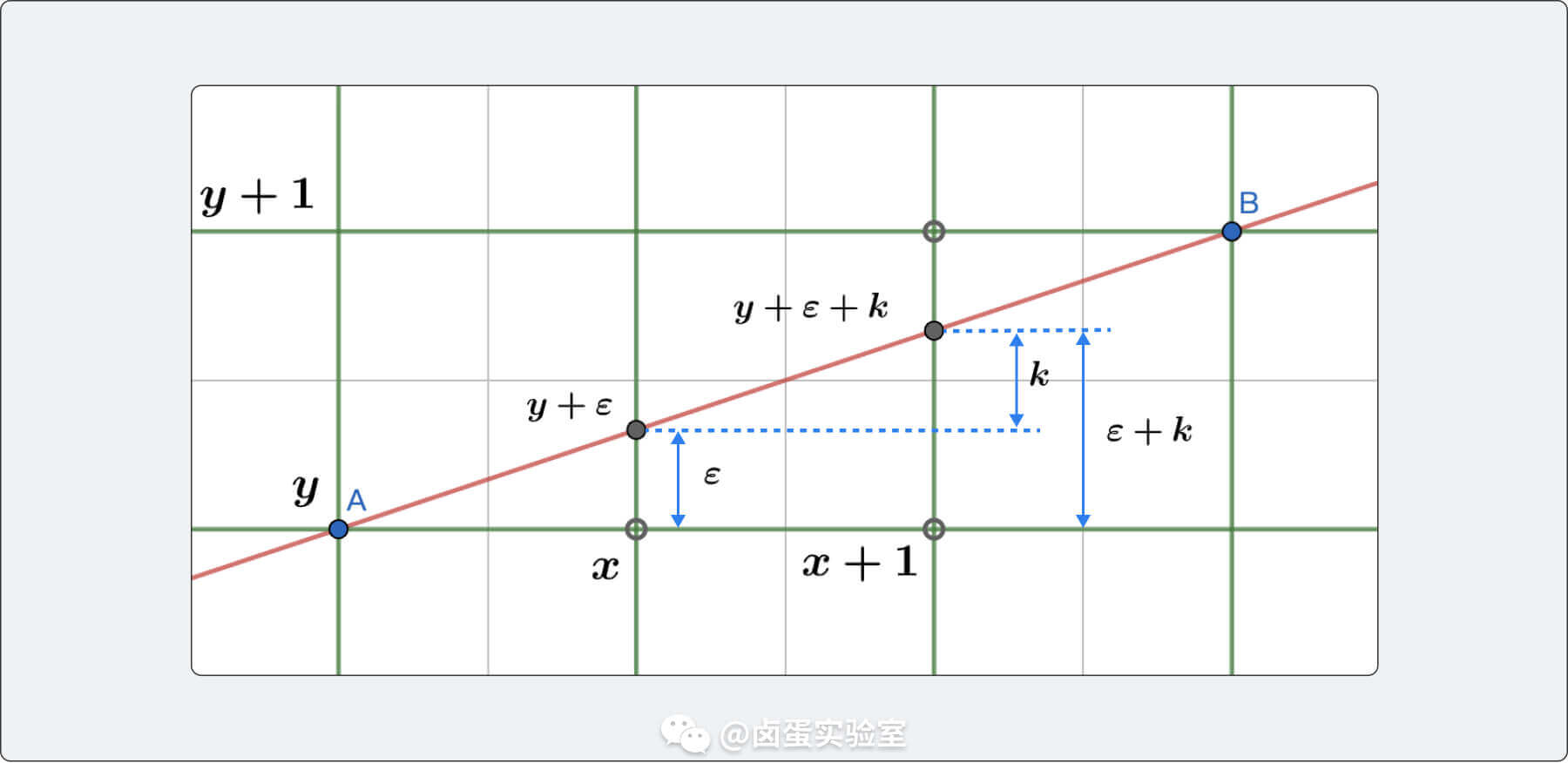
如上图所示，实际上绘制的点的位置是，理论上点位置是。

当点从移动到时，理论上新点的位置应该是，其中 k 是直线的斜率。

实际绘制时，要比较和的大小：

，选点
，选点

对于下一个新点，我们可以按照下式更新误差：

若前一个点选择的是，则
若前一个点选择的是，则

把上面的思考过程用伪代码表示一下：

2.2 消除浮点运算

观察上面的伪代码，我们可以发现这里面出现了 0.5，也就是说存在浮点运算。下面我们就通过一些等价的数学变换消除浮点数。

首先对于不等式，我们给它不等号左右两边同时乘以 2 倍的 ，这样就可以同时消除斜率除法和常量 0.5 带来的浮点运算:

然后用表示，上式可以转换为

同样的，我们在更新时，把它也替换为，也就是对于下面两式：

等号两边同时乘以，有：

然后用表示，可以得到：

这时候我们就可以得到一个去掉浮点数运算的伪代码：

C++ 实现如下：

void line(Screen &s,
  int x1, int y1,
  int x2, int y2,
  TGAImage &image, TGAColor color) {
  int y = y1;
  int eps = 0;
  int dx = x2 - x1;
  int dy = y2 - y1;

  for (int x = x1; x <= x2; x++) {
    image.set(x, y, color);
    eps += dy;
    // 这里用位运算 <<1 代替 *2
    if((eps << 1) >= dx)  {
      y++;
      eps -= dx;
    }
  }
}

这样我们就实现了斜率在区间的高效算法。也就是说，现在我们可以绘制 1/8 个象限的直线了。剩下范围的直线，可以通过交换 xy 等方式实现绘制。具体的实现都是些脏活累活，就不摆出来了，感兴趣的可以去 GitHub 上看代码的完整实现。

3.绘制模型

这一部分可以结合原英文教程学习，我只做一些细节上的补充。

前面两个小节都是算法基础学习，本小节开始加载一个非洲人的 .obj 模型，然后把模型上每个三角形面的点连接起来。

OBJ 文件是一种被广泛使用的 3D 模型文件格式（obj 为后缀名），用来描述一个三维模型。模型关键字较为繁琐，限于篇幅本文暂不展开，大家可以自行搜索学习。

这一节的流程也很清楚：从磁盘上加载 .obj 文件 → 按行分析 .obj 文件 → 构建 model → 循环 model 中的每个三角形 → 连接三角形的三条边 → 渲染出图

上诉流程的前三步已经被原作者封装好了，我们直接把源码里的 model.h 和 model.cpp 拖到主工程里就可以了，感兴趣的人可以看一下源码实现，非常简单，在一个 while 循环里一直 readline 就可以了，因为和图形学关系不大，我这里就略过了。

最后的画三角形的代码如下，关键步骤我已经用注释标注了：

// 实例化模型
model = new Model("obj/african_head.obj");

// 循环模型里的所有三角形
for (int i = 0; i < model->nfaces(); i++) {
  std::vector<int> face = model->face(i);

  // 循环三角形三个顶点，每两个顶点连一条线
  for (int j = 0; j < 3; j++) {
    Vec3f v0 = model->vert(face[j]);
    Vec3f v1 = model->vert(face[(j + 1) % 3]);
    
    // 因为模型空间取值范围是 [-1, 1]^3，我们要把模型坐标平移到屏幕坐标中
    // 下面 (point + 1) * width(height) / 2 的操作学名为视口变换（Viewport Transformation）
    int x0 = (v0.x + 1.) * width / 2.;
    int y0 = (v0.y + 1.) * height / 2.;
    int x1 = (v1.x + 1.) * width / 2.;
    int y1 = (v1.y + 1.) * height / 2.;
    
    // 画线
    line(x0, y0, x1, y1, image, white);
  }
}

最后渲染出的图像如下：

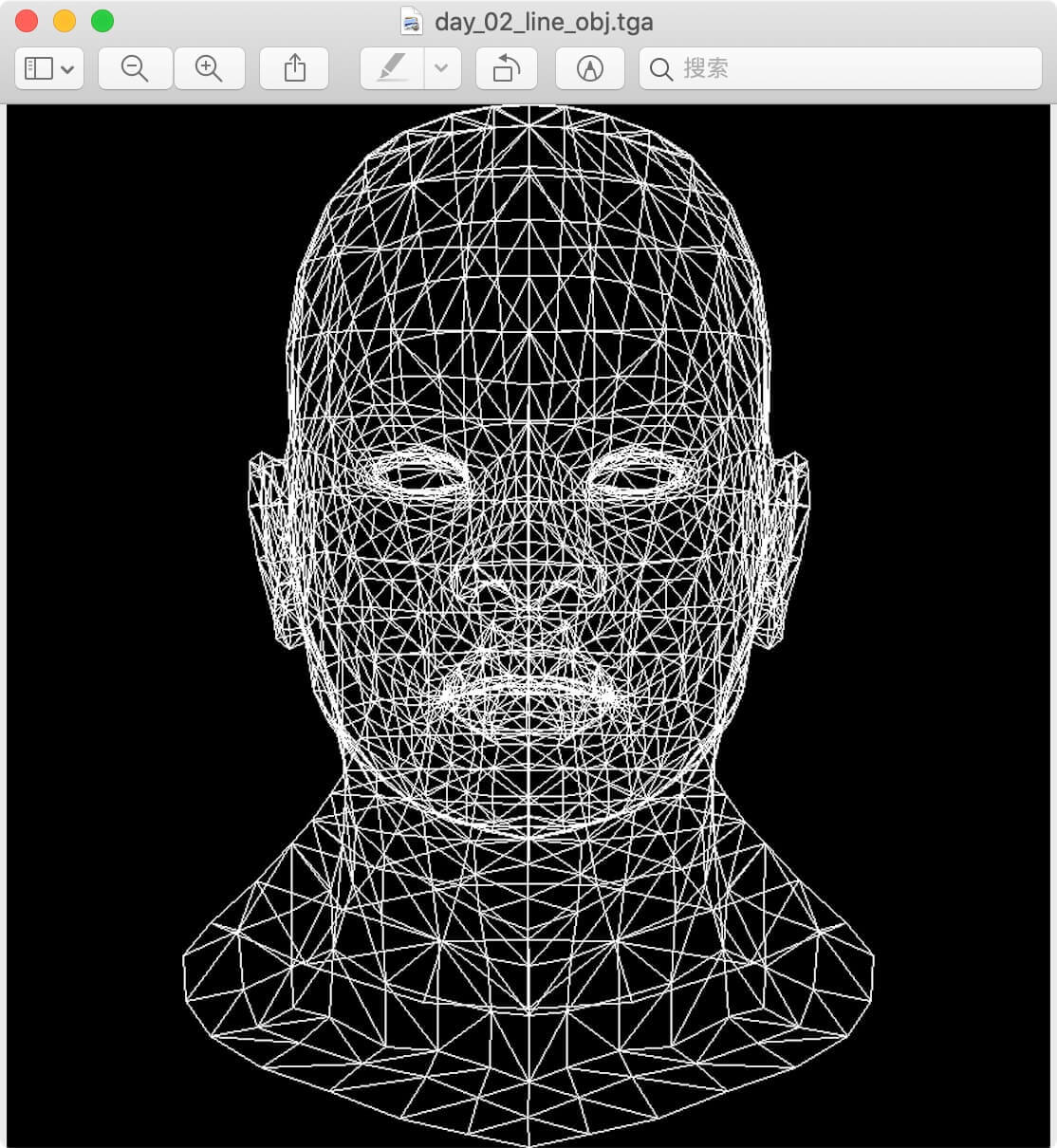
今天学习了如何画一条线，明天我们学习如何画一个三角形。

参考连接：

Line Drawing on Raster Displays

The Bresenham Line-Drawing Algorithm

DDA Line Drawing Algorithm - Computer Graphics

Bresenham's Line Drawing Algorithm

欢迎大家关注我的微信公众号：卤蛋实验室，目前专注前端技术，对图形学也有一些微小研究。

也可以加我的微信 egg_labs，欢迎大家来撩。