证明RSA算法在明文和公私钥中N不互质情况下仍然成立

关于RSA的基础过程介绍

下文中的 k 代表自然数常数，不同句子，公式中不一定代表同一个数

之前接触RSA，没有过多的思考证明过程，今天有感而发，推到了一遍

假设公钥 (e, N) , 私钥 (d, N) ，那么 ed =  k * g (N) + 1 ， g是欧拉函数，假设 N = p * q ，p 和 q 都是 大素数， 那么 g (N) = ( p - 1 ) * ( q - 1 ) , k 是自然数

假设明文是 M , 那么 密文 C = M ^ e (mod N)

密文再次运算的结果是明文，即使明文 R = C ^ d ( mod N ) = ( M ^ e ) ^ d ( mod N ) = M ^ (ed) (mod N)

最后 明文 R = M ^ (ed) (mod N) = M ^ ( k * g(N) + 1 ) ( mod N )

要从 R 推出明文，就要证明 R 和 明文 M 模N 同余，也就是 R = k * N + M (k 为自然数)

很简单的一种情况是 明文 M 和 N 是互质的，因为根据欧拉定理 ：

如果 下图的 a 和 n 互质，则有

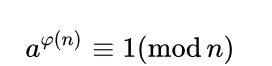
如果 M 和 N 互质，则两边乘 M

　 M ^ ( k * g(N)) 1 (mod N )     =》 [ M ^ ( k * g(N)) ] * [ M ] = M ^ ( k * g(N) + 1 )  = R M ( mod N )

如果 M 和 N 不是互质，就比较难证明了

M 和 N 不互质，那么 M 和 N 必然有一个非1的公因子 ， 假设为 g , 则 N = k1 * g , M = k2 * g (k1, k2 均是常数)

　两个素数相乘的积，只有四个因子，分别是 两个乘起来的素数，1，还有积本身。

　那么 g 就应该是 这四个因子中的一个，前提已经假设 g 非1，那么 g 可能是剩下三个中的一个。

　但是根据 RSA 规范：

　5.1.1RSAEP

　　RSAEP ((n, e), m)

　　Input: (n, e) RSA public key

　　m message representative, an integer between 0 and n– 1

　　Output: c ciphertext representative, an integer between 0 and n– 1

　M 应该小于 N，那么 g 就不能取 N，否则 M =  k * g = k * N > N　

　在当前上下文，N = p * q ,　　p 和 q 就是 那两个大素数， N 就是乘积，那么 g 就应该是 p 或 q ，可以推出 M = k0 * g = k * q 或者 M = k * p  （k0，k 是自然数）

（g是M和N的非1公因子，所以可以写成 M = k0 * g 的形式）

　因为 M < N , 假如 M = k * p , 那么 k = M / p < N / p = q ，也即 k < q ，那么 k 必然和 q 互质，因为 q 是素数 （原因见下图）。M = k * q 时同理

（k 和 q） 与 p 都互质，则有 k * q 与 p 互质。（因为 q 是素数，那么 k * q 分解的话只能分解出 k 和 q，必然没有 p 的因子，下同理）

或者  （k 和 p） 与 q 都互质，则有 k * p 与 q 互质。

再用一次欧拉定理，下面假设 M = k * p

　　(k * p) ^ (g(q)) 1 (mod q)

　 因为 q 是素数，比 q 小的数都和 q 互质，所以有 q - 1 个数 和 q 互质，也就是 q 的欧拉函数运算结果 g (q) = q - 1

也就是：

　　(k * p) ^ (q - 1) 1 (mod q)

　下面还要用到一个推到：

　　假如 A 1 (mod q)  （公式1），那么 ( A ) ^ h 1 (mod q) （公式2）

　　推到：　由公式1得到 A = k * q + 1 , 将 A 代入公式2， ( k * q + 1 ) ^ h 在展开后，只有最后一项是1，不带 k * q，其他都带 k * q , 所以 A^h = ( k * q + 1 ) ^ h 在 mod q 之后还是等于1

　　所以公式2成立

　把 A 换成 (k * p) ^ (q - 1) , h 换成 k0 * (p - 1)

　(k * p) ^ (q - 1) 1 (mod q) 　

可以转化成

　[ ( k * p ) ^ ( q - 1) ] ^ ( k0 * ( p - 1 )) 1 (mod q)

　[ ( k * p ) ] ^ [ k0 * ( q - 1) * ( p - 1 )] 1 (mod q)

　根据 ed = i * g(N) + 1 = i * (p - 1) * (q - 1) + 1

　[ ( k * p ) ] ^ (ed - 1) 1 (mod q)

　两边同乘 k * p

　[ ( k * p ) ] ^ (ed) (k * p) (mod q)

可以写成:

　[ ( k * p ) ] ^ (ed) = (k * p) + k1 * q (k1 是自然数常数)

那么

[ ( k )  ^ (ed) ] * [ p ^ (ed ) ] = (k * p) + k1 * q

[ ( k )  ^ (ed) ] * [ p ^ (ed ) ] - k * p = k1 * q

　[ [ (k) ^ (ed) ] * [ p ^ (ed - 1) ] - k ] * p = k1 * q

　左边是 p 的倍数，右边应该也是 p 的倍数，又 p 和 q 互质，那么只能 k1 是 p 的倍数

　回到之前的公式，把 k1 = k2 * p 代入

　[ ( k * p ) ] ^ (ed) = (k * p) + k1 * q 　　=》 　　 [ ( k * p ) ] ^ (ed) = (k * p) + k2 * p * q

　因为 N = p * q，继续代入

　[ ( k * p ) ] ^ (ed) = (k * p) + k2 * N

[ ( k * p ) ] ^ (ed)   ( mod N ) = [(k * p) + k2 * N ] (mod N) = (k * p) (mod N)

　M = k * p 也就是

　M ^ (ed) (Mod N) = M (mod N)

　也就是 M ^ (ed) 和 M 模 N 同余

也即，R = M ^ (ed) 和 M 同余

　证毕