Paperfolding HDU - 6822

传送门：https://vjudge.net/problem/HDU-6822

题意：给你一张无限的纸有四种折叠方式，并且在n次折叠后减两刀问最后纸张数量的数学期望。

思路：我们要得到一个通项公式对于不同折叠情况下的最后所得纸张数量，因为从上往下对折和从下往上对折是一样的，同理从左忘右对折和从右往左对折也是一样的那么假设从上往下对折k次那么从左往右对折n-k次，那么横线有2^k+1条竖线有2^n-k+1条，因为最后是从中心位置横竖减两刀，所以最后的纸片数量就是（2^k+1)*(2^n-k+1)个。接下来就是对二项式定理的化简了。

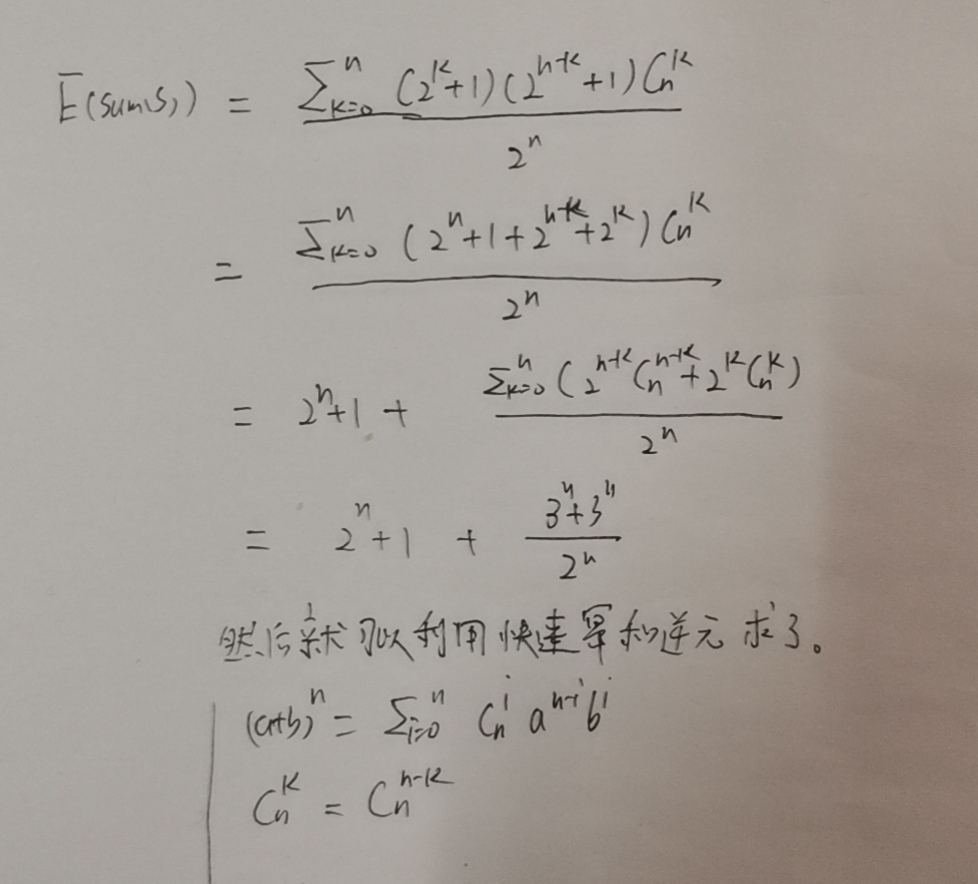
 1 //#include<bits/stdc++.h>
 2 #include<time.h>
 3 #include <set>
 4 #include <map>
 5 #include <stack>
 6 #include <cmath>
 7 #include <queue>
 8 #include <cstdio>
 9 #include <string>
10 #include <vector>
11 #include <cstring>
12 #include <utility>
13 #include <cstring>
14 #include <iostream>
15 #include <algorithm>
16 #include <list>
17 using namespace std;
18 #define eps 1e-10
19 #define PI acos(-1.0)
20 #define lowbit(x) ((x)&(-x))
21 #define zero(x) (((x)>0?(x):-(x))<eps)
22 #define mem(s,n) memset(s,n,sizeof s);
23 #define ios {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);}
24 typedef long long ll;
25 typedef unsigned long long ull;
26 const int maxn=6e6+5;
27 const int Inf=0x7f7f7f7f;
28 const ll Mod=1e9+7;
29 const int N=3e3+5;
30 bool isPowerOfTwo(int n) { return n > 0 && (n & (n - 1)) == 0; }//判断一个数是不是 2 的正整数次幂
31 int modPowerOfTwo(int x, int mod) { return x & (mod - 1); }//对 2 的非负整数次幂取模
32 int getBit(int a, int b) { return (a >> b) & 1; }// 获取 a 的第 b 位，最低位编号为 0
33 int Max(int a, int b) { return b & ((a - b) >> 31) | a & (~(a - b) >> 31); }// 如果 a>=b,(a-b)>>31 为 0，否则为 -1
34 int Min(int a, int b) { return a & ((a - b) >> 31) | b & (~(a - b) >> 31); }
35 ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
36 ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
37 int Abs(int n) {
38   return (n ^ (n >> 31)) - (n >> 31);
39   /* n>>31 取得 n 的符号，若 n 为正数，n>>31 等于 0，若 n 为负数，n>>31 等于 -1
40      若 n 为正数 n^0=n, 数不变，若 n 为负数有 n^(-1)
41      需要计算 n 和 -1 的补码，然后进行异或运算，
42      结果 n 变号并且为 n 的绝对值减 1，再减去 -1 就是绝对值 */
43 }
44 ll binpow(ll a, ll b,ll c) {
45   ll res = 1;
46   while (b > 0) {
47     if (b & 1) res = res * a%c;
48     a = a * a%c;
49     b >>= 1;
50   }
51   return res%c;
52 }
53 void extend_gcd(ll a,ll b,ll &x,ll &y)
54 {
55     if(b==0) {
56         x=1,y=0;
57         return;
58     }
59     extend_gcd(b,a%b,x,y);
60     ll tmp=x;
61     x=y;
62     y=tmp-(a/b)*y;
63 }
64 ll mod_inverse(ll a,ll m)
65 {
66     ll x,y;
67     extend_gcd(a,m,x,y);
68     return (m+x%m)%m;
69 }
70 ll eulor(ll x)
71 {
72    ll cnt=x;
73    ll ma=sqrt(x);
74    for(int i=2;i<=ma;i++)
75    {
76     if(x%i==0) cnt=cnt/i*(i-1);
77     while(x%i==0) x/=i;
78    }
79    if(x>1) cnt=cnt/x*(x-1);
80    return cnt;
81 }
82 int mod=998244353;
83 int main()
84 {
85     ios
86     int T;
87     ll n;
88     cin>>T;
89     while(T--)
90     {
91        cin>>n;
92        ll c2=binpow(2,n,mod);
93        ll c3=binpow(3,n,mod);
94        ll c22=binpow(c2,mod-2,mod);
95        cout<<(1+c2+2*c3*c22)%mod<<endl;
96     }
97     return 0;
98 }