poj3070 (斐波那契，矩阵快速幂)

Fibonacci

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 9630		Accepted: 6839

Description

In the Fibonacci integer sequence, F₀ = 0, F₁ = 1, and F_n = F_{n − 1} + F_{n − 2} for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

.

Given an integer n, your goal is to compute the last 4 digits of F_n.

Input

The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.

Output

For each test case, print the last four digits of F_n. If the last four digits of F_n are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print F_n mod 10000).

Sample Input

0
9
999999999
1000000000
-1

Sample Output

0
34
626
6875

Hint

As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by

.

Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:

.

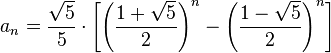求斐波那契序列的公式。

由于该矩阵的特殊结构使得a(n+1)[0][0] = a(n)[0][0]+a(n)[0][1], a(n+1)[0][1] = a(n)[1][1], a(n+1)[1][0] = a(n)[0][1]+a(n)[1][0], a(n+1)[1][1] = a(n)[1][0];

code:

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<vector>
 #include<algorithm>
 #include<cmath>
 #define M(a,b) memset(a,b,sizeof(a))

 using namespace std;

 int n;
 struct matrix
 {
     int a[][];
     void init()
     {
         a[][] = a[][] = a[][] = ;
         a[][] = ;
     }
 };

 matrix mamul(matrix a,matrix b)
 {
     matrix c;
     for(int i = ;i<;i++)
     {
         for(int j = ;j<;j++)
         {
             c.a[i][j] = ;
             for(int k = ;k<;k++)
                 c.a[i][j]+=(a.a[i][k]*b.a[k][j]);
             c.a[i][j]%=;
         }
     }
     return c;
 }

 matrix mul(matrix s, int k)
 {
     matrix ans;
     ans.init();
     while(k>=)
     {
         if(k&)
             ans = mamul(ans,s);
         k = k>>;
         s = mamul(s,s);
     }
     return ans;
 }

 int main()
 {
     while(scanf("%d",&n)==&n>=)
     {
         if(n==) puts("");
         else
         {
             matrix ans;
             ans.init();
             ans = mul(ans,n-);
             printf("%d\n",ans.a[][]%);
         }
     }
     return ;
 }

下面代码只是测试公式，无法解决取模的问题，因为中间为double型，无法取模：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<vector>
 #include<algorithm>
 #include<cmath>
 #define M(a,b) memset(a,b,sizeof(a))

 using namespace std;

 double Pow(double a,int n)
 {
     double ans = ;
     while(n>=)
     {
         if(n&)
             ans = a*ans;
         n = n>>;
         a = a*a;
     }
     return ans;
 }

 int main()
 {
    int n;
    double a = (sqrt(5.0)+1.0)/;
    double b = (-sqrt(5.0)+1.0)/;
    double c = (sqrt(5.0))/;
    while(scanf("%d",&n)==)
    {
         int ans = (int)(c*(Pow(a,n)-Pow(b,n)))%;
         printf("%d\n",ans);
    }
    return ;
 }