[KOJ6997]旅行商问题二

[COJ6997]旅行商问题二

试题描述

Bob是一名旅行商，Bob同时也是一个哲学家，他深知到了一个地方就要掏出钱包把所有景点都玩到。一个城市有N个景点，其中N-1条无向道路链接成一个连通图。Bob出来带的经费是有限的，他希望从1号景点出发，把所有景点都走到(不必返回1点)。每个点不一定只走一次，但是要保证从一号点游览完所有景点的路程最小，他希望你告诉他这个路程。

输入

第一行：一个数N，表示有N个景点(包括1点)
下面N-1行：每行表示一条边，A，B，C表示A点到B点有一条长度为C的边。

输出

游览完所有点的最小路程。

输入示例

输出示例

数据规模及约定

N<=1000

题解

搞一个树形 dp，设 f(i) 表示对于子树 i，遍历一遍所有节点但不回到节点 i 的最短路长度；g(i) 表示遍历一遍子树 i 且回到节点 i 的最短长度。

那么显然

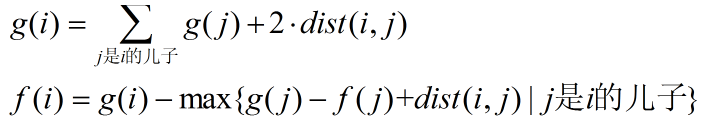
最后答案是 f(1)。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <queue>
#include <cstring>
#include <string>
#include <map>
#include <set>
using namespace std;

int read() {
    int x = 0, f = 1; char c = getchar();
    while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
    while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
    return x * f;
}

#define maxn 1010
#define maxm 2010
int n, m, head[maxn], next[maxm], to[maxm], dist[maxm];

void AddEdge(int a, int b, int c) {
	to[++m] = b; dist[m] = c; next[m] = head[a]; head[a] = m;
	swap(a, b);
	to[++m] = b; dist[m] = c; next[m] = head[a]; head[a] = m;
	return ;
}

int f[maxn], g[maxn];
void dp(int u, int fa) {
	g[u] = 0;
	int tmp = 0;
	for(int e = head[u]; e; e = next[e]) if(to[e] != fa) {
		dp(to[e], u);
		g[u] += g[to[e]] + 2 * dist[e];
		tmp = max(tmp, g[to[e]] - f[to[e]] + dist[e]);
	}
	f[u] = g[u] - tmp;
	return ;
}

int main() {
	n = read();
	for(int i = 1; i < n; i++) {
		 int a = read(), b = read(), c = read();
		 AddEdge(a, b, c);
	}

	dp(1, 0);

	printf("%d\n", f[1]);

	return 0;
}

并不知道数据范围为什么这么小