Linear Algebra - Determinant（几何意义）

二阶行列式的几何意义

二阶行列式 \(D = \begin{vmatrix}a_1&a_2\\b_1&b_2\end{vmatrix} = a_1b_2 - a_2b_1\) 的几何意义是以向量 \(\vec a = (a_1, a_2), \vec b = (b_1, b_2)\) 为邻边的平行四边形的有向面积。

Figure 1. 二阶行列式的几何意义

根据以上条件，知四边形的面积 \(S(\vec a, \vec b) = ab \sin{<\vec a, \vec b>}\)

其中，\(a = \sqrt{a_1^2 + a_2^2}\) ， \(b = \sqrt{b_1^2 + b_2^2}\) ，

\(\sin{<\vec a, \vec b>} = \sin{(\alpha - \beta)} = \sin{\alpha}\cos{\beta} - \cos{\alpha}\sin{\beta} = \frac{b_2}{b} \frac{a_1}{a} - \frac{b_1}{b} \frac{a_2}{b} = \frac{a_1b_2 - a_2b_1}{ab}\)

整理，得 \(ab \sin{<\vec a, \vec b>} = a_1b_2 - a_2b_1\)

而 \(\begin{vmatrix}a_1&a_2\\b_1&b_2\end{vmatrix} = a_1b_2 - a_2b_1\)

所以
\[
\begin{vmatrix}a_1&a_2\\b_1&b_2\end{vmatrix} = S(\vec a, \vec b)
\]

三阶行列式的几何意义

三行列式是其行向量或列向量所张成的平行六面体的有向体积。

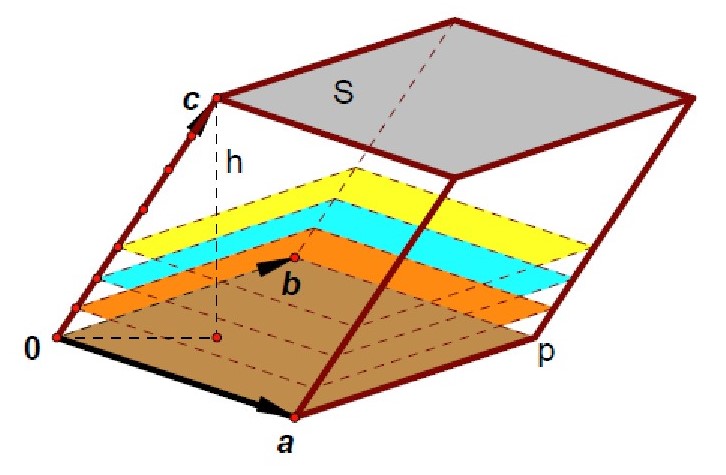
Figure 2. 三阶行列式的几何意义