luogu2805 [NOI2009]植物大战僵尸

想象一下，要搞掉一个植物，必须先搞掉另一些植物……我们可以发现这是一个最大权闭合子图的问题。

最大权闭合子图的话，太空飞行计划问题是一个入门题，可以一看。

然而我们手玩一下样例就会惊恐地发现，保护关系出现了环。

比如说：



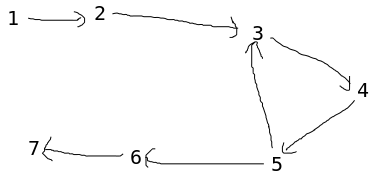
从 i 到 j 的箭头是说要搞 i 就要先搞 j，这是为了和最大权闭合子图的模型对应。

要搞 3 就要先搞 4，要搞 4 就要先搞 5，要搞 5 就要先搞 3……简直是乱来……

这就像是一个无冷却食人花前面放一个坚果

所以就要删环了，把边倒过来拓扑排序一下，能被拓扑到的点就是合法的点。

然后就按照最大权闭合子图的套路搞一搞就是了。

记得开当前弧优化

#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
using namespace std;
int n, m, src[25][35], oea[605], ont, uu, vv, ind[605], ss, tt, tot, maxFlow, cnt, hea[605];
int lev[605], cur[605];
const int oo=0x3f3f3f3f;
queue<int> d;
bool vis[605];
struct Odge{
	int too, nxt;
}odge[370005];
struct Edge{
	int too, nxt, val;
}edge[800005];
int f(int i, int j){
	return (i-1)*m+j;
}
void add_odge(int fro, int too){
	odge[++ont].nxt = oea[fro];
	odge[ont].too = too;
	oea[fro] = ont;
}
void add_edge(int fro, int too, int val){
	edge[cnt].nxt = hea[fro];
	edge[cnt].too = too;
	edge[cnt].val = val;
	hea[fro] = cnt++;
}
void addEdge(int fro, int too, int val){
	add_edge(fro, too, val);
	add_edge(too, fro, 0);
}
void topsort(){
	for(int i=1; i<=n*m; i++)
		if(!ind[i])
			d.push(i);
	while(!d.empty()){
		int x=d.front();
		d.pop();
		vis[x] = true;
		for(int i=oea[x]; i; i=odge[i].nxt){
			int t=odge[i].too;
			ind[t]--;
			if(!ind[t])
				d.push(t);
		}
	}
}
bool bfs(){
	memset(lev, 0, sizeof(lev));
	lev[ss] = 1;
	d.push(ss);
	while(!d.empty()){
		int x=d.front();
		d.pop();
		for(int i=hea[x]; i!=-1; i=edge[i].nxt){
			int t=edge[i].too;
			if(!lev[t] && edge[i].val>0){
				lev[t] = lev[x] + 1;
				d.push(t);
			}
		}
	}
	return lev[tt]!=0;
}
int dfs(int x, int lim){
	if(x==tt)	return lim;
	int addFlow=0;
	for(int &i=cur[x]; i!=-1; i=edge[i].nxt){
		int t=edge[i].too;
		if(lev[t]==lev[x]+1 && edge[i].val>0){
			int tmp=dfs(t, min(lim-addFlow, edge[i].val));
			edge[i].val -= tmp;
			edge[i^1].val += tmp;
			addFlow += tmp;
			if(addFlow==lim)    break;
		}
	}
	return addFlow;
}
void dinic(){
	while(bfs()){
		for(int i=ss; i<=tt; i++)	cur[i] = hea[i];
		maxFlow += dfs(ss, oo);
	}
}
int main(){
	memset(hea, -1, sizeof(hea));
	cin>>n>>m;
	for(int i=1; i<=n; i++)
		for(int j=1; j<=m; j++){
			scanf("%d", &src[i][j]);
			int tmp;
			scanf("%d", &tmp);
			while(tmp--){
				scanf("%d %d", &uu, &vv);
				uu++; vv++;
				add_odge(f(i,j), f(uu,vv));
				ind[f(uu,vv)]++;
			}
			if(j>1)	add_odge(f(i,j), f(i,j-1)), ind[f(i,j-1)]++;
		}
	topsort();
	for(int i=1; i<=n; i++)
		for(int j=1; j<=m; j++)
			if(vis[f(i,j)])
				for(int k=oea[f(i,j)]; k; k=odge[k].nxt){
					int t=odge[k].too;
					if(vis[t])
						addEdge(t, f(i,j), oo);
				}
	ss = 0; tt = n * m + 1;
	for(int i=1; i<=n; i++)
		for(int j=1; j<=m; j++)
			if(vis[f(i,j)]){
				if(src[i][j]>=0)	addEdge(ss, f(i,j), src[i][j]), tot += src[i][j];
				else	addEdge(f(i,j), tt, -src[i][j]);
			}
	dinic();
	cout<<max(tot-maxFlow, 0)<<endl;
	return 0;
}