java实现哈夫曼编码

java实现哈夫曼编码

哈夫曼树

  既然是学习哈夫曼编码，我们首先需要知道什么是哈夫曼树：给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

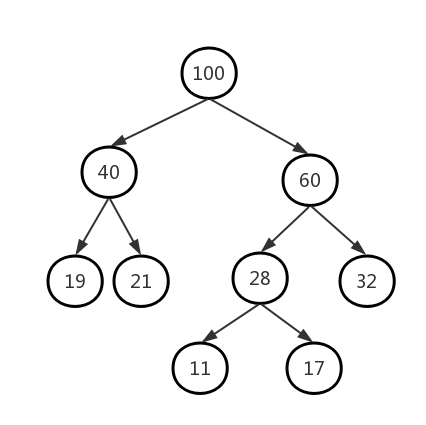
哈夫曼编码

  在日常计算机的使用中，我们一定会出现下面这种情况：假如给定a、b、c、d、e五个字符，它们在文本中出现的概率如下图所示：

字符	概率
a	0.12
b	0.40
c	0.15
d	0.05
e	0.25

我们现在要将文本编码成0/1序列从而使得计算机能够进行读取和计算。为了保证每个字符的独一性，所以我们给予不同的的字符以不同的编码。如果给每个字符赋予等长的编码的话，会使得平均的编码长度过长，影响计算时的性能，浪费计算机的资源(定长编码的缺点)。这时我们就想到了变长编码，理所当然的，给出现概率较大的字符赋予较短的编码，概率较小的字符赋予较长的编码，这样在计算的时候不就可以节省很多时间了吗？可这样我们又面临到了一个巨大的问题，我们来看下面这种情况，我们对字符进行编码：

字符	概率	编码
a	0.12	01
b	0.40	0
c	0.15	00
d	0.05	10
e	0.25	1

  假设现在文本中的字符是bcd，转换之后的0/1序列为00010，可我们要在转换成文本的时候究竟是把第一位的0读作b还是把前两位的00读作c呢？为了解决这个问题，就又有了前缀码的概念。顾名思义，前缀码的含义就是任意字符的编码都不是其他字符编码的前缀。那么该如何形成前缀码呢？首先我们要构造一棵二叉树，指向左孩子的"边"记作0,指向右孩子的点记作“1”，叶子节点为代编码的字符，出现概率越大的字符离根的距离就越近。

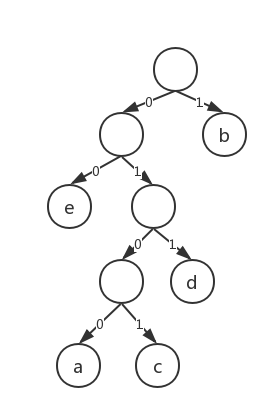
字符	概率	编码
a	0.12	0100
b	0.40	1
c	0.15	0101
d	0.05	011
e	0.25	00

  我们在前面提到：哈夫曼树的带权路径最小，所以有哈夫曼树构成的前缀码记作哈夫曼编码。哈夫曼作为已知的最佳无损压缩算法，满足前缀码的性质，可以即时解码。

哈夫曼编码（Huffman Coding），又称霍夫曼编码，是一种编码方式，哈夫曼编码是可变字长编码（VLC）的一种。Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫做Huffman编码（有时也称为霍夫曼编码）。

java代码实现

  实现哈夫曼编码的主要思路为从指定的文件中读出文本，首先通过遍历获得各个字符出现的概率，根据出现概率的大小构造二叉树，在此基础上进行编码解码。

• 首先来构造哈夫曼树的结点类，在结点类中有老生常谈的变量数据data、权重weight、指向左孩子的指针left、指向右孩子的指针right。除此之外，为了在构造了哈夫曼树之后容易对data进行编码，在这里我还使用了一个变量code来储存0/1字符。
  
  

public class Node<T> implements Comparable<Node<T>> {
    private T data;
    private double weight;
    private Node<T> left;
    private Node<T> right;
    String code;

    public Node(T data, double weight){
        this.data = data;
        this.weight = weight;
        this.code = "";

    }

    public T getData() {
        return data;
    }

    public void setData(T data) {
        this.data = data;
    }

    public double getWeight() {
        return weight;
    }

    public void setWeight(double weight) {
        this.weight = weight;
    }

    public Node<T> getLeft() {
        return left;
    }

    public void setLeft(Node<T> left) {
        this.left = left;
    }

    public Node<T> getRight() {
        return right;
    }

    public void setRight(Node<T> right) {
        this.right = right;
    }

    public String getCode(){
        return code;
    }

    public void setCode(String str){
        code = str;
    }

    @Override
    public String toString(){
        return "data:"+this.data+";weight:"+this.weight+";code: "+this.code;
    }

    @Override
    public int compareTo(Node<T> other) {
        if(other.getWeight() > this.getWeight()){
            return 1;
        }
        if(other.getWeight() < this.getWeight()){
            return -1;
        }

        return 0;
    }
}

• 紧接着我们来构建哈夫曼树。
  • createTree方法返回一个结点，也就是根结点。首先把所有的nodes结点类都储存在一个List中，利用Collections的sort方法把结点按照权值的大小按照从大到小的顺序进行排列。然后把List中的倒数第二个元素设为左孩子，倒数第一个元素设为右孩子。这个时候要注意:它们的双亲结点为以左右孩子的权值的和作为权值的构成的新的结点。然后删去左右孩子结点，将形成的新结点加入的List中。直到List中只剩下一个结点，也就是根结点时为止。

public Node<T> createTree(List<Node<T>> nodes) {
        while (nodes.size() > 1) {
            Collections.sort(nodes);

            Node<T> left = nodes.get(nodes.size() - 2);
            left.setCode(0 + "");
            Node<T> right = nodes.get(nodes.size() - 1);
            right.setCode(1 + "");
            Node<T> parent = new Node<T>(null, left.getWeight() + right.getWeight());
            parent.setLeft(left);
            parent.setRight(right);
            nodes.remove(left);
            nodes.remove(right);
            nodes.add(parent);
        }
        return nodes.get(0);
    }

• 在构建哈夫曼树的类中还实现了一个广度遍历的方法,在遍历的时候，每遍历到左孩子，就把结点中的code变量加上“0”，这里的加不是简单的数学运算，而是字符串的叠加。每遍历到右孩子，就把结点中的code变量加上“1”，这样遍历过一遍后，叶子结点中的code储存的就是对应的哈夫曼编码值。

 public List<Node<T>> breadth(Node<T> root) {
        List<Node<T>> list = new ArrayList<Node<T>>();
        Queue<Node<T>> queue = new ArrayDeque<Node<T>>();

        if (root != null) {
            queue.offer(root);
            root.getLeft().setCode(root.getCode() + "0");
            root.getRight().setCode(root.getCode() + "1");
        }

        while (!queue.isEmpty()) {
            list.add(queue.peek());
            Node<T> node = queue.poll();
            if (node.getLeft() != null)
                node.getLeft().setCode(node.getCode() + "0");
            if (node.getRight() != null)
                node.getRight().setCode(node.getCode() + "1");

            if (node.getLeft() != null) {
                queue.offer(node.getLeft());
            }

            if (node.getRight() != null) {
                queue.offer(node.getRight());
            }
        }
        return list;
    }

• 接下来我们首先从指定的文件中读取文本：

File file = new File("G:/usually/input/input1.txt");

• 这里我们还需要构造一个类对读取的文本进行处理：chars数组储存的是文本中所有可能的字符，number数组中储存的是文本中所有字符出现的次数，这里我所申请的number数组的长度为27，为什么是27呢？因为在这里加上了空格。在num方法中利用双循环对字符进行计数，在这里不再过多赘述。

public class readtxt {
    char[] chars = new char[]{'a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s'
                                  ,'t','u','v','w','x','y','z',' '};
    int[] number = new int[]{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0};
    public String txtString(File file){
        StringBuilder result = new StringBuilder();
        try{
            BufferedReader br = new BufferedReader(new FileReader(file));//构造一个BufferedReader类来读取文件
            String s = null;
            while((s = br.readLine())!=null){//使用readLine方法，一次读一行
                result.append(System.lineSeparator()+s);
                num(s);
            }
            br.close();
        }catch(Exception e){
            e.printStackTrace();
        }
        return result.toString();
    }

    public void num(String string){
        for(int i = 0;i<27;i++){
            int temp = 0;
            for(int j = 0;j<string.length();j++){
                if(string.charAt(j) == chars[i])
                    temp++;
            }
            number[i] += temp;
        }
    }

    public int[] getNumber(){
        return number;
    }

    public char[] getChars(){
        return chars;
    }
}

• 调用上面readtxt中的方法对文本进行处理,定义两个数组获得文本中出现的字符和字符出现的次数。

        readtxt read = new readtxt();
        String temp = read.txtString(file);
        int[] num = read.getNumber();
        char[] chars = read.getChars();

• 利用一个循环把对应的data值和weight权重值构造成结点加入到list中。

for(int i = 0;i<27;i++){
            System.out.print(chars[i]+"："+num[i]+"   ");
            list.add(new Node<String>(chars[i]+"",num[i]));
        }

• 构建哈夫曼树并得到根结点。

        HuffmanTree huffmanTree = new HuffmanTree();
        Node<String> root = huffmanTree.createTree(list);

• 调用哈夫曼树中广度遍历方法，在建立两个新的list用来储存遍历之后的字符以及相对应的哈夫曼编码。

list2=huffmanTree.breadth(root);
        for(int i = 0;i<list2.size();i++){
            if(list2.get(i).getData()!=null) {
                list3.add(list2.get(i).getData());
                list4.add(list2.get(i).getCode());
            }
        }

• 对从指定文本中读出的数据进行遍历，并与list3中的字符进行比较，如若相等，则转换为对应的变码。直至遍历结束，哈夫曼编码完成。

for(int i = 0;i<temp.length();i++){
            for(int j = 0;j<list3.size();j++){
                if(temp.charAt(i) == list3.get(j).charAt(0))
                    result += list4.get(j);
            }
        }

• 在解码的过程中我在这里选择了用一个list5把已编码完成的字符串分开来储存，然后对list5在进行遍历，从list5中取出一位元素temp2与list4中对应的编码进行比对，如果没有相同的，再从list5中读取一位加到temp2的后面，如果有，则清空temp2。每次找到相同的，就把对应的字符加到temp3的后面，直至整个list5遍历结束，temp3即为解码后的结果。

for(int i = 0;i<result.length();i++){
            list5.add(result.charAt(i)+"");
        }
        while (list5.size()>0){
            temp2 = temp2+"" +list5.get(0);
            list5.remove(0);
            for(int i=0;i<list4.size();i++){
                if (temp2.equals(list4.get(i))) {
                    temp3 = temp3+""+list3.get(i);
                    temp2 = "";
                }
            }
        }

• 写入文件，大功告成！

File file2 =new File("G:/usually/input/input2.txt");
        Writer out =new FileWriter(file2);
        out.write(temp3);
        out.close();

  最后得到的结果：

完整代码