C# 实现二叉树各种排序

1. 引言

在实际的项目中，树还是用的比较多的一种，尤其是对于具有层次结构的数据。相信很多人都学过树的遍历，比如先序遍历，后序遍历等，利用递归还是很容易理解的。

今天给大家介绍下二叉树的几种遍历算法，包括递归和非递归的实现。

首先建立一棵二叉树 如：

        [DebuggerDisplay("Value={Value}")]
        public class Tree
        {
            public string Value;
            public Tree Left;
            public Tree Right;
        }

        public static Tree CreatFakeTree()
        {
            Tree tree = new Tree() {Value = "A"};
            tree.Left = new Tree()
            {
                Value = "B",
                Left = new Tree() {Value = "D", Left = new Tree() {Value = "G"}},
                Right = new Tree() {Value = "E", Right = new Tree() {Value = "H"}}
            };
            tree.Right = new Tree() {Value = "C", Right = new Tree() {Value = "F"}};

            return tree;
        }

一棵简单的二叉树

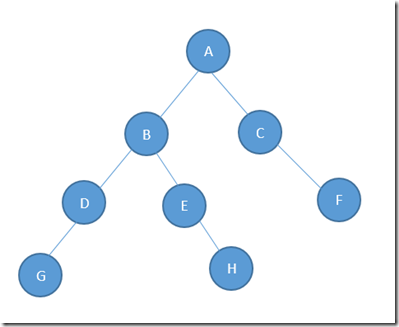
2. 先序遍历

先序遍历还是很好理解的，一次遍历根节点，左子树，右子数

递归实现

        public static void PreOrder(Tree tree)
        {
            if (tree == null)
                return;

            System.Console.WriteLine(tree.Value);
            PreOrder(tree.Left);
            PreOrder(tree.Right);
        }

非递归实现

        public static void PreOrderNoRecursion(Tree tree)
        {
            if(tree == null)
                return;

            System.Collections.Generic.Stack<Tree> stack = new System.Collections.Generic.Stack<Tree>();
            Tree node = tree;

            while (node != null || stack.Any())
            {
                if (node != null)
                {
                    stack.Push(node);
                    System.Console.WriteLine(node.Value);
                    node = node.Left;
                }
                else
                {
                    var item = stack.Pop();
                    node = item.Right;
                }
            }
        }

输出结果：

3. 中序遍历

递归实现

        public static void InOrder(Tree tree)
        {
            if(tree == null)
                return;

            InOrder(tree.Left);
            System.Console.WriteLine(tree.Value);
            InOrder(tree.Right);
        }

非递归实现

        public static void InOrderNoRecursion(Tree tree)
        {
            if (tree == null)
                return;

            System.Collections.Generic.Stack<Tree> stack = new System.Collections.Generic.Stack<Tree>();
            Tree node = tree;

            while (node != null || stack.Any())
            {
                if (node != null)
                {
                    stack.Push(node);
                    node = node.Left;
                }
                else
                {
                    var item = stack.Pop();
                    System.Console.WriteLine(item.Value);

                    node = item.Right;
                }
            }
        }

输出结果：

4. 后序遍历

递归实现

        public static void PostOrder(Tree tree)
        {
            if (tree == null)
                return;

            PostOrder(tree.Left);
            PostOrder(tree.Right);
            System.Console.WriteLine(tree.Value);
        }

非递归实现 比前两种稍微复杂一点。要保证左右节点都被访问后，才能访问根节点。这里给出两种形式。

        public static void PostOrderNoRecursion(Tree tree)
        {
            if (tree == null)
                return;

            System.Collections.Generic.Stack<Tree> stack = new System.Collections.Generic.Stack<Tree>();
            Tree node = tree;
            Tree pre = null;
            stack.Push(node);

            while (stack.Any())
            {
                node = stack.Peek();
                if ((node.Left == null && node.Right == null) ||
                    (pre != null && (pre == node.Left || pre == node.Right)))
                {
                    System.Console.WriteLine(node.Value);
                    pre = node;

                    stack.Pop();
                }
                else
                {
                    if(node.Right != null)
                        stack.Push(node.Right);

                    if(node.Left != null)
                        stack.Push(node.Left);
                }
            }
        }

        public static void PostOrderNoRecursion2(Tree tree)
        {
            HashSet<Tree> visited = new HashSet<Tree>();
            System.Collections.Generic.Stack<Tree> stack = new System.Collections.Generic.Stack<Tree>();
            Tree node = tree;

            while (node != null || stack.Any())
            {
                if (node != null)
                {
                    stack.Push(node);
                    node = node.Left;
                }
                else
                {
                    var item = stack.Peek();
                    if (item.Right != null && !visited.Contains(item.Right))
                    {
                        node = item.Right;
                    }
                    else
                    {
                        System.Console.WriteLine(item.Value);
                        visited.Add(item);
                        stack.Pop();
                    }
                }
            }
        }

输出结果:

5. 层序遍历

层序遍历就是按照层次由左向右输出

        public static void LevelOrder(Tree tree)
        {
            if(tree == null)
                return;

            Queue<Tree> queue = new Queue<Tree>();
            queue.Enqueue(tree);

            while (queue.Any())
            {
                var item = queue.Dequeue();
                System.Console.Write(item.Value);

                if (item.Left != null)
                {
                    queue.Enqueue(item.Left);
                }

                if (item.Right != null)
                {
                    queue.Enqueue(item.Right);
                }
            }
        }

输出结果：

6. Z-型层序遍历

Z-层序遍历就是奇数层按照由左向右输出，偶数层按照由右向左输出，这里定义了几个辅助函数，比如计算节点所在的层次。算法思想是按照层次保存树形节点，应该是有更加优化的算法，希望大家指出。

        public static int GetDepth(Tree tree, Tree node)
        {
            if (tree == null)
                return ;

            if (tree == node)
                return ;

            if (tree.Left == node || tree.Right == node)
                return ;

            int lDepth = GetDepth(tree.Left, node);
            lDepth = lDepth ==  ?  : lDepth + ;

            int rDepth = GetDepth(tree.Right, node);
            rDepth = rDepth ==  ?  : rDepth + ;

            return lDepth >= rDepth ? lDepth : rDepth;
        }

        public static void Z_LevelOrder(Tree tree, Dictionary<int, List<Tree>> dictionary)
        {
            if (tree == null)
                return;

            Queue<Tree> queue = new Queue<Tree>();
            queue.Enqueue(tree);

            while (queue.Any())
            {
                var item = queue.Dequeue();
                var depth = GetDepth(tree, item);

                List<Tree> list;
                if (!dictionary.TryGetValue(depth, out list))
                {
                    list = new List<Tree>();
                    dictionary.Add(depth, list);
                }
                list.Add(item);

                if (item.Left != null)
                {
                    queue.Enqueue(item.Left);
                }

                if (item.Right != null)
                {
                    queue.Enqueue(item.Right);
                }
            }
        }

        public static void Z_LevelOrder(Tree tree)
        {
            if (tree == null)
                return;

            Dictionary<int, List<Tree>> dictionary = new Dictionary<int, List<Tree>>();
            Z_LevelOrder(tree, dictionary);

            foreach (KeyValuePair<int, List<Tree>> pair in dictionary)
            {
                if (pair.Key% == )
                {
                    pair.Value.Reverse();
                }

                pair.Value.ForEach(t=> { System.Console.Write(t.Value); });
            }
        }

输出结果：