POJ 1063 - Flip and Shift

Description

This puzzle consists of a random sequence of m black disks and n white disks on an oval-shaped track, with a turnstile capable of flipping (i.e., reversing) three consecutive disks. In Figure 1, there are 8 black disks and 10 white disks on the track. You may spin the turnstile to flip the three disks in it or shift one position clockwise for each of the disks on the track (Figure 1). 

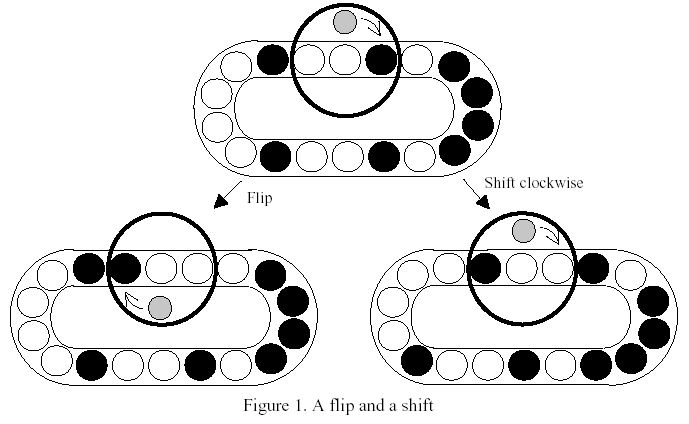
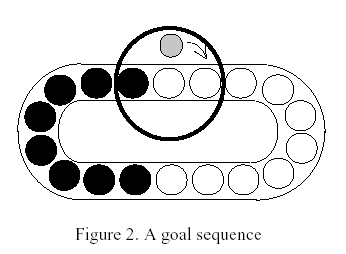
The goal of this puzzle is to gather the disks of the same color in adjacent positions using flips and shifts. (Figure 2) 

You are to write a program which decides whether a given sequence can reach a goal or not. If a goal is reachable, then write a message "YES"; otherwise, write a message "NO".

Input

The input consists of T test cases. The number of test cases ) (T is given in the first line of the input file. Each of the next T lines gives a test case. A test case consists of an integer, representing the sum of m and n, and a sequence of m+n 0s and 1s, representing an initial sequence. A 0 denotes a white disk and a 1 denotes a black disk. The sum of m and n is at least 10 and does not exceed 30. There is a space between numbers.

Output

The output should print either "YES" or "NO" for each test case, one per line.

Sample Input

2
18 0 0 1 0 1 1 1 1 0 1 0 0 1 0 0 0 0 1
14 1 1 0 0 1 1 1 0 0 1 1 0 1 0

Sample Output

YES
NO

Source

Taejon 2001

 

不算水题，搞清楚原理后属于简单题。

当总的个数n为odd时，任何一个球都能到达圆圈中的每一个位置，所以就是YES。

当总的个数n为even时，那么如果这个球的位置在odd位置上，那么它能到任意一个odd位置，若在even位置上，则能到任意一个even位置。

那么不妨把黑球全部移到一起，不去管白球，那么如果偶数位置的黑球更多一些，中间就夹着少一个的奇数的空位，把剩下的那些奇数个黑球放进去，如果 even - odd = 0 or 1 ，那么这个时候是可以把空位放满的，否则就放不满，即NO；类似的如果odd位置的黑球更多一点，就判断odd - even = 0 or 1是否为真即可。

 #include<stdio.h>
 #include<stdlib.h>
 int main()
 {
 　　int even,odd;
 　　int i,n,disk[],T;scanf("%d",&T);
 　　while(T){
 　　　　scanf("%d",&n);
 　　　　for(i=;i<n;i++) scanf("%d",&disk[i]);
 　　　　if( n% ==  ) printf("YES\n"); //n为odd，必然YES
 　　　　else{
 　　　　　　even=,odd=; //初始化even位和odd位的黑球数
 　　　　　　for(i=;i<n;i++){
 　　　　　　　　if( disk[i]== && i%== ) odd++; //odd位黑球计数
 　　　　　　　　if( disk[i]== && i%== ) even++; //even位黑球计数
 　　　　}
 　　　　if(abs(odd-even)>) printf("NO\n"); //判断"|odd - even| = 0 or 1"是否成立
 　　　　else printf("YES\n");
 　　}
 　　T--;
 　　}
 }