根据lame定理，根据欧几里得算法求(a,b)的最大公因数过程如下(假设a>b)：

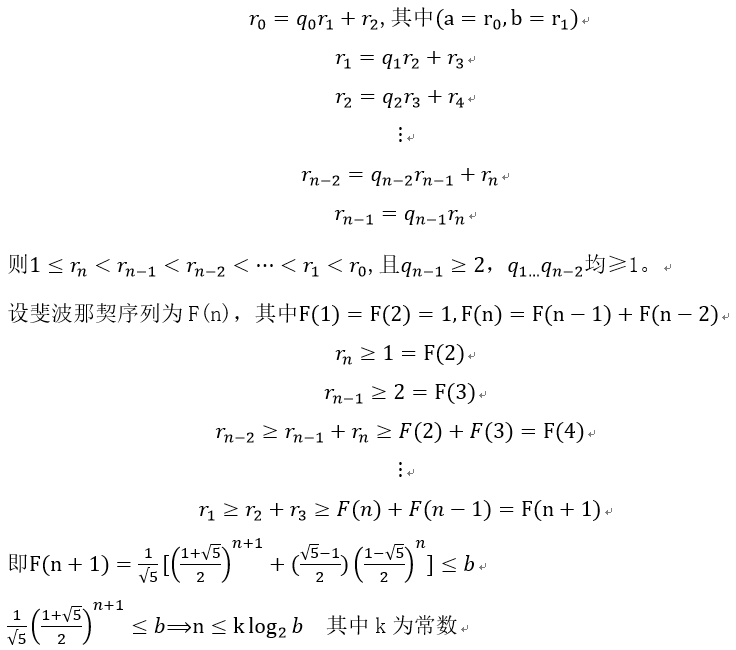
lame定理求欧几里得算法的求余和赋值次数的更多相关文章

  1. 初等数论-Base-2(扩展欧几里得算法，同余，线性同余方程，(附：裴蜀定理的证明))

    我们接着上面的欧几里得算法说 扩展欧几里得算法 扩展欧几里德算法是用来在已知a, b求解一组x,y,使它们满足贝祖等式\(^①\): ax+by = gcd(a, b) =d(解一定存在,根据数论中的 ...

  2. 模板——扩展欧几里得算法（求ax+by=gcd的解）

    Bryce1010模板 /**** *扩展欧几里得算法 *返回d=gcd(a,b),和对应等式ax+by=d中的x,y */ long long extend_gcd(long long a,long ...

  3. 欧几里得算法（gcd） 裴蜀定理 拓展欧几里得算法（exgcd）

    欧几里得算法 又称辗转相除法 迭代求两数 gcd 的做法 由 (a,b) = (a,ka+b) 的性质:gcd(a,b) = gcd(b,a mod b) int gcd(int a,int b){ ...

  4. 【初等数论】裴蜀定理&扩展欧几里得算法

    裴蜀定理: 对于\(a,b\in N^*, x, y\in Z\),方程\(ax+by=k\)当且仅当\(gcd(a, b)|k\)时有解. 证明: 必要性显然. 充分性:只需证明当\(k=gcd(a ...

  5. 扩展欧几里得算法（EXGCD）学习笔记

    0.前言 相信大家对于欧几里得算法都已经很熟悉了.再学习数论的过程中,我们会用到扩展欧几里得算法(exgcd),大家一定也了解过.这是本蒟蒻在学习扩展欧几里得算法过程中的思考与探索过程. 1.Bézo ...

  6. [算法]求满足要求的进制(辗转相除（欧几里得算法），求最大公约数gcd)

    题目 3在十进制下满足若各位和能被3整除,则该数能被3整除. 5在十六进制下也满足此规律. 给定数字k,求多少进制(1e18进制范围内)下能满足此规律,找出一个即可,无则输出-1. 题解 写写画画能找 ...

  7. 欧几里得算法求最大公约数（gcd）

    关于欧几里得算法求最大公约数算法, 代码如下: int gcd( int a , int b ) { if( b == 0 ) return a ; else gcd( b , a % b ) ; } ...

  8. 浅谈欧几里得算法求最大公约数(GCD)的原理及简单应用

    一.欧几里得算法及其证明 1.定义: 欧几里得算法又称辗转相除法,用于求两数的最大公约数,计算公式为GCD(a,b)=GCD(b,a%b): 2.证明: 设x为两整数a,b(a>=b)的最大公约 ...

  9. 欧几里得算法求最大公约数-《Algorithms Fourth Edition》第1章

    最大公约数(Greatest Common Divisor, GCD),是指2个或N个整数共有约数中最大的一个.a,b的最大公约数记为(a, b).相对应的是最小公倍数,记为[a, b]. 在求最大公 ...

随机推荐

  1. linux常用文本编缉命令(strings/sed/awk/cut)

    一.strings strings--读出文件中的所有字符串 二.sed--文本编缉 类型 命令 命令说明 字符串替换 sed -i 's/str_reg/str_rep/' filename 将文件 ...

  2. 接收上传的multi-file的文件(四)

    构建工程 为例创建一个springmvc工程你需要spring-boot-starter-thymeleaf和 spring-boot-starter-web的起步依赖.为例能够上传文件在服务器,你需 ...

  3. python 小白学习（1）

    自定义错误类型 class XxxError(Exception): def __init__(self , message): self = Exception("xxxxx") ...

  4. CString 转换为 wchar_t *

    1.将CString转换为const char* CString str = _T("231222"); std::string strDp = CStringA(str);  / ...

  5. bzoj1679

    题解: 前缀和 显然需要排序一下 注意爆int这件事 代码: #include<bits/stdc++.h> using namespace std; typedef long long ...

  6. Date和 Calendar

    import java.text.ParseException; import java.text.SimpleDateFormat; import java.util.Calendar; impor ...

  7. 深入研究sqlalchemy连接池

    简介: 相对于最新的MySQL5.6,MariaDB在性能.功能.管理.NoSQL扩展方面包含了更丰富的特性.比如微秒的支持.线程池.子查询优化.组提交.进度报告等. 本文就主要探索MariaDB当中 ...

  8. QuickHit 项目

    package cn.javaoppday01; import java.util.Random; public class Game { public Player player; public G ...

  9. dns资源记录类型

    资源记录的定义格式: 语法:name [TTL] IN RR_TYPE value SOA: name:当前区域的名字,例如"magedu.com.",或者"2.168. ...

  10. div 自适应高度

    自适应高度 ,设置最小高度:通常情况下,没有设置高度,div默认自适应高度且无最低高度 1 div{ _height:200px; /* css 注解: 仅IE6设别此属性,假定最低高度是200px ...