differential related impedance and termination

Impedance

(1) Z0

Z0 is the impedance of one T-line while other lines are held at 0.

Single end.

(2) Zdiff

Zdiff is the impedance bw T1 and T2.

when lines are uncoupled,

Zdiff = 2* Z0;

(3) Zcomm

Zcomm is defined as the current that flows in the pair due to Vcomm.

Vcomm on T1 and T2 are the same, so it can be seen as T1 and T2 are connected together.

so when there’s no couple,

Zcomm = 1/2* Z0;

(4) Zodd

Zodd is the impedance of a single trace, when the pair is driven with an ODD Mode.

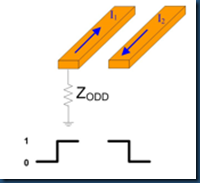
If there’s no coupling,   Zdiff = 2* Z0;

if there’s coupling, Zdiff = 2* Zodd.

(5) Zeven

Zeven is the impedance of a single trace, when the pair is driven with an EVEN Mode.

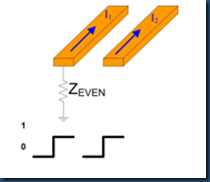
If there’s no coupling,   Zcomm = 1/2 * Z0;

if there’s coupling, Zcomm = 1/2 * Zeven.

(6 ) commom equations to calculate Z0, Zodd and Zeven:

Termination

We want to create a termination network that:

1) Vdiff observes Zdiff = 2·ZODD, that is Zdiff is constant;
2) Vcomm observes Zcomm = (1/2)·Zeven, that is Zcomm is constant.

For a single ODD or EVEN case, it can be accomplished by:

1) for ODD mode

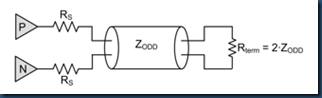
2) for EVEN mode

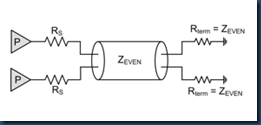
But obviouly none of above can cover both cases.

To cover both cases, we can use Pie network or T network.

(1) Pie network

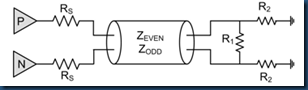
. for EVEN mode, voltages on both ends of R1 are Vcomm, so R1 can be seen as open, hence

R2 = Zeven

. for ODD mode, we hope:

R1//(2*R2) = 2* Zodd.

It can be transferred as:

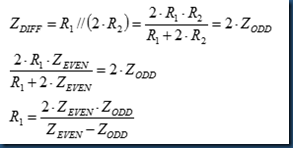
In summary, for Pie termination network,

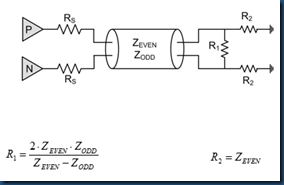
(2) T network

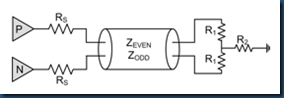
. for ODD mode, there’s a virtual ground at the connecting point of R1 and R2, so R2 can be seen as obsolete, hence

R1 = Zodd.

. for EVEN mode, we hope:

1/2* R1 + R2 = 1/2 * Zeven,

it can be transferred as:

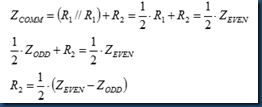
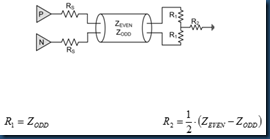
In summary, for T termination network: