基于python的二分搜索和例题

二分搜索

二分概念

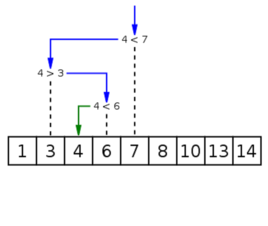
二分搜索是一种在有序数组中查找某一特定元素的搜索算法。

搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；

如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。

如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。

注意

二分搜索或者说二分查找应该注意的几个点：

1. 区间的开闭：左闭右闭，还是左闭右开
2. 循环条件：left<right，还是left<=right，实际和第一点是呼应的
3. 更新条件：左右区间的更新，同样要对应开闭原则，维持区间的循环不变性
4. 返回值：返回left或right，还是需要再判断
5. 搜索条件：大于，等于，小于，大于等于，小于等于

例题

以下是一些二分搜索的一些例题，请细品！

01. 在旋转之后的列表查找最小值

假设有一个升序排列的数列在某个未知节点处被前后调换，请找到数列中的最小值
例如：[4, 5, 6, 7, 1, 2, 3]

def search_min(li):
    if len(li) == 0:
        return -1

    left, right = 0, len(li) - 1
    while left + 1 < right:
        # 左边小于右边，证明有序直接返回左边元素
        if li[left] < li[right]:
            return li[left]

        mid = left + (right - left) // 2
        if li[mid] > li[left]:
            left = mid + 1
        else:
            right = mid

    return li[left] if li[left] < li[right] else li[right]

li= [4, 5, 6, 7, 1, 2, 3]
print(search_min(li)) #

02. 旋转列表查找数值

假设有一个升序排列的数列在某个未知节点处被前后调换，请找到数列中的item
例如：在[4, 5, 6, 7, 8, 1, 2, 3] 找 1 返回index 5

def search_item(li, item):
    if len(li) == 0:
        return -1

    left, right = 0, len(li)-1
    while left+1 < right:
        mid = left + (right-left) //2

        if li[mid] == item:
            return mid

        if li[mid] > li[left]:
            if li[mid] >= item and li[left] <= item:
                right = mid
            else:
                left = mid
        else:
            if li[mid] <= item and li[right] >= item:
                left = mid
            else:
                right = mid

    if li[left] == item:
        return left
    elif li[right] == item:
        return right
    else:
        return -1

li= [4, 5, 6, 7, 1, 2, 3]
print(search_item(li, 3)) #

03. 搜索插入位置

给定有序数组和一个目标值，如果在数组中找到此目标值则返回目标值的index，
如果没有找到，则返回目标值按顺序应该被插入的位置index.
注：可以假设数组中不存在重复数。

def search_insert_position(li, item):
    if len(li) == 0:
        return 0

    left, right = 0, len(li) - 1
    while left + 1 < right:
        mid = left + (right - left) // 2
        if li[mid] == item:
            return mid

        if li[mid] < item:
            left = mid
        else:
            right = mid

    if li[left] >= item:
        return left
    if li[right] >= item:
        return right

    return right+1

li= [1, 2, 3, 4, 5, 6, 7]
print(search_insert_position(li, 3)) #

04. 搜索区间

找给定的目标值的开始和结束的位置
例如 给定列表[1, 2, 3, 3, 4, 4, 5, 5, 5, 5, 6, 7, 8, 9], 目标值5，返回(6,9)

def search_range(li, item):
    if len(li) == 0:
        return -1, -1

    # 搜索左边边界
    left, right = 0, len(li) - 1
    while left + 1 < right:
        mid = left + (right - left) // 2
        if li[mid] == item:
            right = mid
        elif li[mid] < item:
            left = mid
        else:
            right = mid

    if li[left] == item:
        left_bound = left
    elif li[right] == item:
        left_bound = right
    else:
        return -1, -1

    # 搜索右边边界
    left, right = 0, len(li) - 1
    while left + 1 < right:
        mid = left + (right - left) // 2
        if li[mid] == item:
            left = mid
        elif li[mid] < item:
            left = mid
        else:
            right = mid

    if li[right] == item:
        right_bound = right
    elif li[left] == item:
        right_bound = left
    else:
        return -1, -1

    return left_bound, right_bound

li = [1, 2, 3, 3, 4, 4, 5, 5, 5, 5, 6, 7, 8, 9]
print(search_range(li, 5)) # (6, 9)

05. 再有空字符串的列表中查找数值

给定一个有序的字符串序列，这个序列中的字符串用空字符隔开，请写出找到给定字符串位置的方法
例如：["", "", 1, "", 3, 4, "", "", "", 5, "", 6, 7, 8, "", ""]

def search_item(li, item):
    if len(li) == 0:
        return -1

    left, right = 0, len(li) - 1

    while left + 1 < right:
        # 去除右边的空字符串
        while left + 1 < right and li[right] == "":
            right -= 1

        if li[right] == "":
            right -= 1

        if right < left:
            return -1

        # 获取mid
        mid = left + (right - left) // 2
        while li[mid] == "":
            mid += 1

        if li[mid] == item:
            return mid

        if li[mid] < item:
            left = mid + 1
        else:
            right = mid - 1

    if li[left] == item:
        return left
    elif li[right] == item:
        return right
    else:
        return -1

li = ["", "", 1, "", 3, 4, "", "", "", 5, "", 6, 7, 8, "", ""]
print(search_item(li, 5)) #

06. 查找某个元素第一次出现的位置

在数据流中常用, 不知道列表长度
例如：[0, 1, 2, 3, 4, 4, 4, 5, 5, 6, 7, 8, 9] 查找5， 返回index 7

def search_first(li, item):
    left, right = 0, 1

    while li[right] < item:
        left = right
        right *= 2

        if right > len(li):
            right = len(li) - 1
            break

    while left + 1 < right:
        mid = left + (right - left) // 2

        if li[mid] == item:
            right = mid
        elif li[mid] < item:
            left = mid
        else:
            right = mid

    if li[left] == item:
        return left
    elif li[right] == item:
        return right
    else:
        return -1

li = [0, 1, 2, 3, 4, 4, 4, 5, 5, 6, 7, 8, 9]
print(search_first(li, 5)) #

07. 供暖设备

冬季来临！你的首要任务是设计一款有固定供暖半径的供暖设备来给所有的房屋供暖。
现在你知道所有房屋以及供暖设备在同一水平线上的位置分布，请找到能给所有房屋供暖的供暖设备的最小供暖半径。
你的输入是每个房屋及每个供暖设备的位置，输出应该是供暖设备的最小半径。

from bisect import bisect

# 找到可以插入的位置
def search_insert_position(li, item):
    if len(li) == 0:
        return 0

    left, right = 0, len(li) - 1
    while left + 1 < right:
        mid = left + (right - left) // 2
        if li[mid] == item:
            return mid

        if li[mid] < item:
            left = mid
        else:
            right = mid

    if li[left] >= item:
        return left
    if li[right] >= item:
        return right

    return right + 1

def findRadius(houses, heaters):
    # 时间复杂度(nlogn)
    heaters.sort()
    ans = 0
    for house in houses:
        # 查找房子可插入供暖设备中的位置, 返回index
        # index = bisect(heaters, h)
        index = search_insert_position(heaters, house)
        # 左边界大于等于0，否则为负无穷
        left = heaters[index - 1] if index - 1 >= 0 else float('-inf')
        right = heaters[index] if index < len(heaters) else float('inf')
        # 先求房子与每一个供暖设备距离的最小值，再求其中的最大值
        ans = max(ans, min(house-left, right-house))
    return ans

houses = [1,2,3,6]
heaters = [1,4]
print(findRadius(houses, heaters)) #

08. 求平方根

例如 输入40，输出6， 6*6<40<7*7

def sqrt(item):
    if item == 0:
        return 0

    left, right = 1, item
    while left <= right:
        mid = left + (right-left) // 2
        if item // mid == mid:
            return mid

        if item // mid > mid:
            left = mid + 1
        else:
            right = mid -1

    return right

print(sqrt(80)) #

09. 找重复数

给定一个包含n+1个整数的数组，其中每个元素为1到n闭区间的整数值，请证明至少存在一个重复数。
假设只有一个重复数，请找到这个重复数。

def find_duplicate(li):
    left = 0
    right = len(li) - 1

    while left < right:
        mid = left + (right - left) // 2
        count = 0
        for i in li:
            if i <= mid:
                count += 1
        if count <= mid:
            left = mid + 1
        else:
            right = mid

    return left

li = [3, 5, 6, 3, 1, 4, 2]
print(find_duplicate(li)) #

10. 合并区间

给定一个区间的集合，将所有存在交叉范围的区间进行合并。
输入: [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
说明: 因为区间 [1,3] 和 [2,6] 存在交叉范围, 所以将他们合并为[1,6]

# 定义区间
class Interval:
    def __init__(self, s=0, e=0):
        self.start = s
        self.end = e

    def __str__(self):
        return f"[{self.start}, {self.end}]"

    def __repr__(self):
        return "[%s, %s]" % (self.start, self.end)

def merge(intervals):
    # 区间按照第一个元素排序
    intervals.sort(key=lambda x: x.start)

    # 定义一个新的列表存放区间
    merged = []
    for interval in intervals:
        # 如果合并区间列表为空或当前区间与上一个区间不重叠，只需附加它即可。
        if not merged or merged[-1].end < interval.start:
            merged.append(interval)
        else:
            # 有重叠将当前区间和上一个区间合并
            merged[-1].end = max(merged[-1].end, interval.end)

    return merged

intervals1 = Interval(1, 3)
intervals2 = Interval(2, 6)
intervals3 = Interval(8, 10)
intervals4 = Interval(15, 18)
intervals = [intervals1, intervals2, intervals3, intervals4]
print(merge(intervals))  # [[1, 6], [8, 10], [15, 18]]

11. 插入区间

给定一个没有交叉范围的区间集合，在这个集合中插入一个新的区间（如果需要，请进行合并）。
你可以认为这些区间已经初始时根据他们的头元素进行过排序
输入：区间集合=[[1,3],[6,9]], 新区间 = [2,5]
输出：[[1,5],[6,9]]

# 定义区间
class Interval:
    def __init__(self, s=0, e=0):
        self.start = s
        self.end = e

    def __str__(self):
        return f"[{self.start}, {self.end}]"

    def __repr__(self):
        return "[%s, %s]" % (self.start, self.end)

def insert(intervals, newInterval):
    merged = []
    for i in intervals:
        if newInterval is None or i.end < newInterval.start:
            merged += i,
        elif i.start > newInterval.end:
            merged += newInterval,
            merged += i,
            newInterval = None
        else:
            newInterval.start = min(newInterval.start, i.start)
            newInterval.end = max(newInterval.end, i.end)
    if newInterval is not None:
        merged += newInterval,
    return merged

intervals1 = Interval(1, 3)
intervals2 = Interval(6, 9)
intervals = [intervals1, intervals2]
new = Interval(2, 5)
print(insert(intervals, new))  # [[1, 5], [6, 9]]

解法..

# 定义区间
class Interval:
    def __init__(self, s=0, e=0):
        self.start = s
        self.end = e

    def __str__(self):
        return f"[{self.start}, {self.end}]"

    def __repr__(self):
        return "[%s, %s]" % (self.start, self.end)

def insert2(intervals, newInterval):
    if len(intervals) == 0:
        intervals += newInterval,

    startPos = searchPosition(intervals, newInterval.start)
    endPos = searchPosition(intervals, newInterval.end)

    newStart = 0

    # case 1:
    # startPos
    #           A
    # |____|    |____|    |____|
    #         <-
    #           startPos is less than A
    # and intervals[startPos].end >= newInterval.start
    # then
    #   new     A
    # |____|    |____|    |____|
    #     <-
    # newInterval starts within ONE interval
    # so newStart = intervals[startPos].start
    if (startPos >= 0 and intervals[startPos].end >= newInterval.start):
        newStart = intervals[startPos].start
    else:
        # case 2:
        # startPos = -1
        # A
        # |____|    |____|    |____|
        # newInterval starts before 1st interval
        # so newStart = newInterval.start

        # case 3:
        # startPos >= 0
        # A    B
        # |____|    |____|    |____|
        # newInterval starts between A and B
        # so NOT intervals[startPos].end >= newInterval.start
        # so newStart = newInterval.start
        newStart = newInterval.start
        startPos += 1

    newEnd = 0
    # case 1:
    # endPos >= 0
    # endPos
    #           A
    # |____|    |____|    |____|
    #         <-
    #           endPos is less than A
    # so newEnd = Math.max(newInterval.end, intervals.get(endPos).end)
    if (endPos >= 0):
        newEnd = max(newInterval.end, intervals[endPos].end)
    else:
        # case 2:
        # endPos < 0
        # endPos
        # A
        #     |____|    |____|    |____|
        #
        # endPos is before 1st interval
        # create a new interval
        newEnd = newInterval.end

    for i in range(startPos, endPos + 1):
        intervals.pop(startPos)  # note: NOT i, but startPos, since one element is removed.

    intervals.insert(startPos, Interval(newStart, newEnd))
    return intervals

# return (actual insertion position - 1)
def searchPosition(intervals, x):
    start = 0
    end = len(intervals) - 1
    while (start <= end):
        mid = start + (end - start) // 2
        if (intervals[mid].start == x):
            return mid
        if (intervals[mid].start < x):
            start = mid + 1
        else:
            end = mid - 1

    return end

2

~>.<~