P1198 [JSOI2008]最大数（线段树）

P1198 [JSOI2008]最大数（线段树）

题目描述

现在请求你维护一个数列，要求提供以下两种操作：

1、 查询操作。

语法：Q L

功能：查询当前数列中末尾L个数中的最大的数，并输出这个数的值。

限制：L不超过当前数列的长度。(L>=0)

2、 插入操作。

语法：A n

功能：将n加上t，其中t是最近一次查询操作的答案（如果还未执行过查询操作，则t=0)，并将所得结果对一个固定的常数D取模，将所得答案插入到数列的末尾。

限制：n是整数（可能为负数）并且在长整范围内。

注意：初始时数列是空的，没有一个数。

输入输出格式

输入格式：

第一行两个整数，M和D，其中M表示操作的个数(M <= 200,000)，D如上文中所述，满足(0<D<2,000,000,000)

接下来的M行，每行一个字符串，描述一个具体的操作。语法如上文所述。

输出格式：

对于每一个查询操作，你应该按照顺序依次输出结果，每个结果占一行。

输入输出样例

输入样例#1： 复制

5 100
A 96
Q 1
A 97
Q 1
Q 2

输出样例#1： 复制

96
93
96

说明

[JSOI2008]

本题数据已加强

分析解答：

这个题目线段树，树状数组，单调栈，分块等方法都可以做；

核心是查找一串数中的最大值。

下面是线段树的解法：

这道题并不需要提前建树，只要按照输入的顺序挨个添加就好啦

要是不会线段树的话，可以先去看一下线段树模板1

运用线段树的算法。首先建树，把所有的节点的值赋成min_int。用[i,j]表示该区间的最大值。

1）读入Q L操作。用len表示区间的大小，在len+1的位置放入（L+T)%D的值。

2）读入A n操作。输出区间[len-n+1,len]这个区间中的最大值，并把t的值进行更新。

得分：100

时间复杂度：O(nlogn)

空间复杂度：O(4*n)

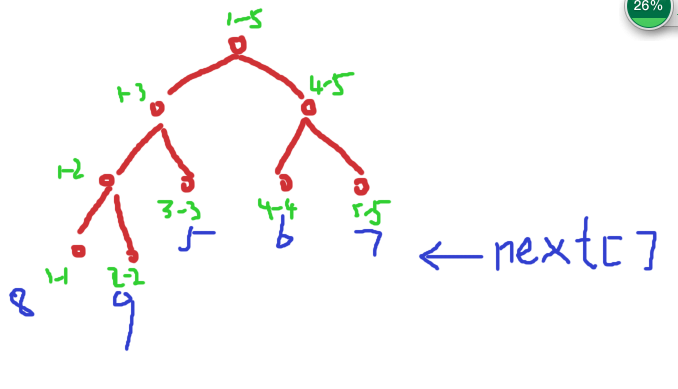
next数组把所有叶子节点的位置都找到了

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 using namespace std;
 struct tree
 {
     int l,r,_max;//左右边界和最大值
 }a[];//4倍空间
 int n,m,d,x,t,next[];
 //建树
 void make_tree(int x,int l,int r)
 {
     a[x].l=l;
     a[x].r=r;
     //叶子节点
     if(l==r)
     {
         //这里x是root
         //next里面记录的是所有叶子节点的位置，或者说编号
         next[l]=x;
         return;
         //这里本来是要做数据的初始化的，但是因为现在数据还没加进来，做不了
     }
     int mid=(l+r)/;
     //左右子树
     make_tree(x*,l,mid);
     make_tree(x*+,mid+,r);
 }
 void add(int x)
 {
     a[next[++n]]._max=(x+t)%d;//这一步就是做叶子节点数据的初始化
     //本来n是0，第一个数是8的位置，那就插到8的位置就好
     int temp=next[n];
     //节点发生改变，肯定要更新父亲节点
     //比如说第一个节点的位置是8，那么temp就是从8 4 2 1，这样一直更新到root节点
     while(a[temp]._max>a[temp/]._max)//子节点大于父亲节点才更新
     {
         //无论是左右孩子，除2都可以得到父亲
         a[temp/]._max=a[temp]._max;
         temp=temp/;
     }
 }
 //查询操作 ，这里的x是根节点 ，y是左边界 ，y是我们要查询的边界的左边界
 int q(int x,int y)
 {
     //包含的情况，因为求最后几个，右边界是固定的
     if(a[x].l>=y) return a[x]._max;
     //没有相交的情况
     if(a[x].r<y) return ;
     //相交又不包含的情况
     //左右孩子中的大值
     return max(q(x*,y),q(x*+,y));
 }
 void print(int m){
     cout<<"i"<<"   "<<"next[i]"<<"  "<<endl;
     for(int i=;i<=*m;i++){
         cout<<i<<"   "<<next[i]<<"  "<<endl;
     }
 }
 int main()
 {
 //    freopen("in.txt","r",stdin);
     cin>>m>>d;
     a[].l=;
     a[].r=m;
     //这里就是左+右除2
     make_tree(,,(m+)/);
     make_tree(,(m+)/+,m);
 //    print(m);
     for(int i=;i<=m;i++)
     {
         char ch;
         cin>>ch;
         cin>>x;
         //插入操作
         if(ch=='A') add(x);
         if(ch=='Q')
         {
             //查询操作，比如x是2，比如5个操作，因为进行了两次插入操作，所以n就是2，q(1,2-2+1)
             //这里的1是root，而n-x+1是我们要查询的左边界，因为右边界不用管
             t=q(,n-x+);
             cout<<t<<endl;
         }
     }
 //    print(m);
 }