Leetcode之并查集专题-765. 情侣牵手（Couples Holding Hands）

Leetcode之并查集专题-765. 情侣牵手（Couples Holding Hands）

---

N 对情侣坐在连续排列的 2N 个座位上，想要牵到对方的手。 计算最少交换座位的次数，以便每对情侣可以并肩坐在一起。 一次交换可选择任意两人，让他们站起来交换座位。

人和座位用 0 到 2N-1 的整数表示，情侣们按顺序编号，第一对是 (0, 1)，第二对是 (2, 3)，以此类推，最后一对是 (2N-2, 2N-1)。

这些情侣的初始座位  row[i] 是由最初始坐在第 i 个座位上的人决定的。

示例 1:

输入: row = [0, 2, 1, 3]
输出: 1
解释: 我们只需要交换row[1]和row[2]的位置即可。

示例 2:

输入: row = [3, 2, 0, 1]
输出: 0
解释: 无需交换座位，所有的情侣都已经可以手牵手了。

说明:

1. len(row) 是偶数且数值在 [4, 60]范围内。
2. 可以保证row 是序列 0...len(row)-1 的一个全排列。

---

有N对情侣，求交换多少次，可以让他们坐在自己该坐的地方。

并查集思路，以示例1为例：

用f数组存储他们的关系，如果x和y为情侣，那么f[y] = x，f[x]=x;

初始状态，每个情侣之间连一条线。

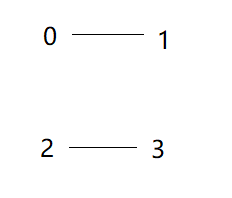
第一步里，f[0]=0,f[1]=0,f[2]=2,f[3]=2;

下一步，按照传入进来数组的顺序，两个两个取出。

先取出0,2，我们在0和2之间连一条线：

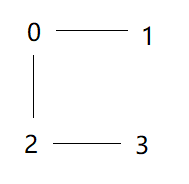
即让f[2] = 0;

再取出1,3，在1和3之间连一条线：

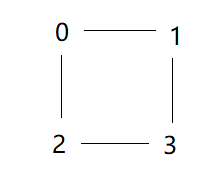
即让f[3]=f[1]=0;

最终成了一个环，我们最后的答案只需要返回 情侣的对数-环数 就可以了。

class Solution {
    int[] f;
    public int minSwapsCouples(int[] row) {
        int len = row.length;
        int res = 0;
        f = new int[len];
        for (int i = 0; i < row.length-1; i+=2) {
            f[i] = i;
            f[i+1] = i;
        }
        for (int i = 0; i < row.length-1; i+=2) {
            int first = row[i];
            int second = row[i+1];
            int father1 = getFather(first);
            int father2 = getFather(second);
            if(father1!=father2){
                f[father2] = father1;
            }else{
                res++;
            }
        }
        return (len/2) - res;
    }

    private int getFather(int i) {
        if(f[i]==i){
            return i;
        }else{
            return getFather(f[i]);
        }
    }
}