The Maze

There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up, down, left or right, but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction.

Given the ball's start position, the destination and the maze, determine whether the ball could stop at the destination.

The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The start and destination coordinates are represented by row and column indexes.

Example 1

Input 1: a maze represented by a 2D array

0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
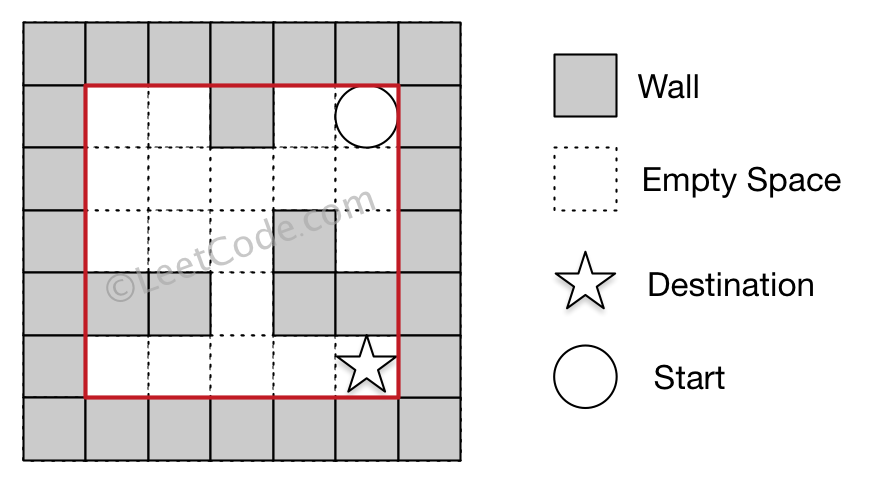
0 0 0 0 0

Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (4, 4)

Output: true
Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.

 

Example 2

Input 1: a maze represented by a 2D array

0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
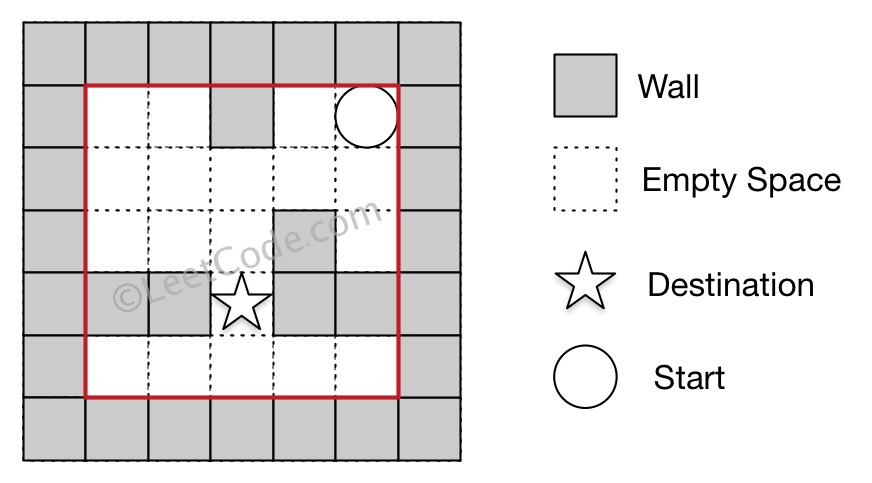
0 0 0 0 0

Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (3, 2)

Output: false
Explanation: There is no way for the ball to stop at the destination.

 

Note:

1. There is only one ball and one destination in the maze.
2. Both the ball and the destination exist on an empty space, and they will not be at the same position initially.
3. The given maze does not contain border (like the red rectangle in the example pictures), but you could assume the border of the maze are all walls.
4. The maze contains at least 2 empty spaces, and both the width and height of the maze won't exceed 100.

DFS

对于dfs，如果当前“决定”对后续有影响，可以使用第16行这种方法不断递归。

 class Solution {
     public boolean hasPath(int[][] maze, int[] start, int[] destination) {
         int m = maze.length, n = maze[].length;
         boolean[][] visited = new boolean[m][n];
         return dfs(maze, visited, start, destination);
     }
     private boolean dfs(int[][] maze, boolean[][] visited, int[] start, int[] destination) {
         int row = start[], col = start[];
         if (row <  || row >= maze.length || col <  || col >= maze[].length || visited[row][col]) return false;
         visited[row][col] = true;
         if (row == destination[] && col == destination[]) return true;

        int[] directions = { , , , -,  };
         for (int i = ; i < directions.length - ; i++) {
             int[] newStart = roll(maze, start[], start[], directions[i], directions[i + ]);
             if (dfs(maze, visited, newStart, destination)) return true;
         }
         return false;
     }

     private int[] roll(int[][] maze, int row, int col, int rowInc, int colInc) {
         while (canRoll(maze, row + rowInc, col + colInc)) {
             row += rowInc;
             col += colInc;
         }
         return new int[]{row, col};
     }

     private boolean canRoll(int[][] maze, int row, int col) {
         if (row >= maze.length || row <  || col >= maze[].length || col <  || maze[row][col] == ) return false;
         return true;
     }
 }

BFS

 class Solution {
     public boolean hasPath(int[][] maze, int[] start, int[] destination) {
         Deque<int[]> queue = new ArrayDeque<>();
         boolean[][] visited = new boolean[maze.length][maze[].length];
         queue.offer(start);
         while (!queue.isEmpty()) {
             int[] cur = queue.poll();
             int row = cur[], col = cur[];
             if (row == destination[] && col == destination[]) {
                 return true;
             }
             if (visited[row][col]) {
                 continue;
             }
             visited[row][col] = true;

             int[] directions = { , , , -,  };
             for (int i = ; i < directions.length - ; i++) {
                 int[] newStart = roll(maze, row, col, directions[i], directions[i + ]);
                 queue.offer(newStart);
             }
         }
         return false;
     }

     private int[] roll(int[][] maze, int row, int col, int rowInc, int colInc) {
         while (canRoll(maze, row + rowInc, col + colInc)) {
             row += rowInc;
             col += colInc;
         }
         return new int[] { row, col };
     }

     private boolean canRoll(int[][] maze, int row, int col) {
         if (row >= maze.length || row <  || col >= maze[].length || col <  || maze[row][col] == )
             return false;
         return true;
     }
 }