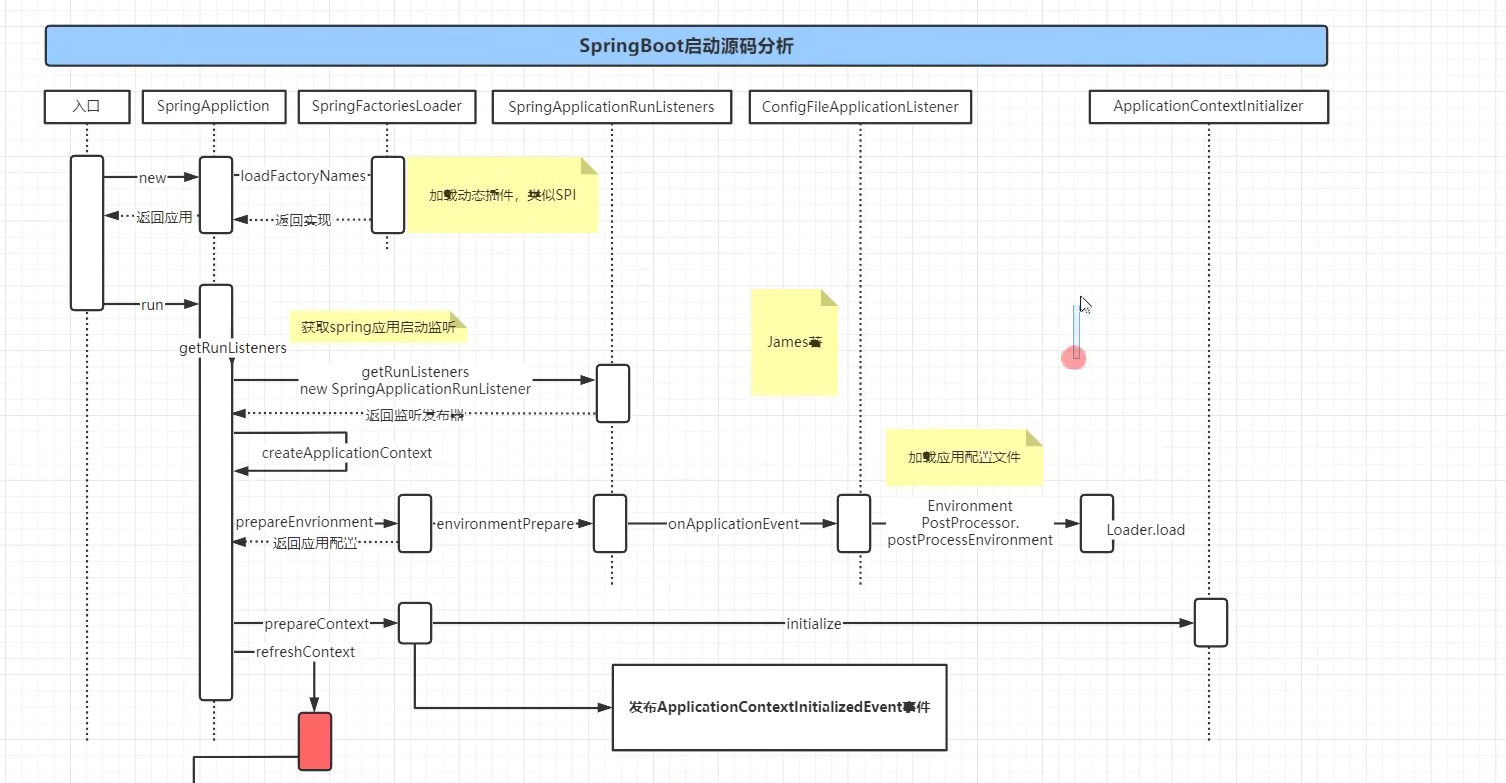
SpringBoot启动源码分析
SpringBoot启动源码分析的更多相关文章
- RocketMQ中Broker的启动源码分析(一)
在RocketMQ中,使用BrokerStartup作为启动类,相较于NameServer的启动,Broker作为RocketMQ的核心可复杂得多 [RocketMQ中NameServer的启动源码分 ...
- RocketMQ中Broker的启动源码分析(二)
接着上一篇博客 [RocketMQ中Broker的启动源码分析(一)] 在完成准备工作后,调用start方法: public static BrokerController start(Broker ...
- RocketMQ中PullConsumer的启动源码分析
通过DefaultMQPullConsumer作为默认实现,这里的启动过程和Producer很相似,但相比复杂一些 [RocketMQ中Producer的启动源码分析] DefaultMQPullCo ...
- Django如何启动源码分析
Django如何启动源码分析 启动 我们启动Django是通过python manage.py runsever的命令 解决 这句话就是执行manage.py文件,并在命令行发送一个runsever字 ...
- 【原创】005 | 搭上SpringBoot请求处理源码分析专车
前言 如果这是你第二次看到师长,说明你在觊觎我的美色! 点赞+关注再看,养成习惯 没别的意思,就是需要你的窥屏^_^ 专车介绍 该趟专车是开往Spring Boot请求处理源码分析专车,主要用来分析S ...
- Seata AT 模式启动源码分析
从上一篇文章「分布式事务中间件Seata的设计原理」讲了下 Seata AT 模式的一些设计原理,从中也知道了 AT 模式的三个角色(RM.TM.TC),接下来我会更新 Seata 源码分析系列文章. ...
- Quartz源码——scheduler.start()启动源码分析(二)
scheduler.start()是Quartz的启动方式!下面进行分析,方便自己查看! 我都是分析的jobStore 方式为jdbc的SimpleTrigger!RAM的方式类似分析方式! Quar ...
- Netty源码分析 (三)----- 服务端启动源码分析
本文接着前两篇文章来讲,主要讲服务端类剩下的部分,我们还是来先看看服务端的代码 /** * Created by chenhao on 2019/9/4. */ public final class ...
- 【原创】002 | 搭上SpringBoot事务源码分析专车
前言 如果这是你第二次看到师长,说明你在觊觎我的美色! 点赞+关注再看,养成习惯 没别的意思,就是需要你的窥屏^_^ 专车介绍** 该趟专车是开往Spring Boot事务源码分析的专车 专车问题 为 ...
- Netty服务端的启动源码分析
ServerBootstrap的构造: public class ServerBootstrap extends AbstractBootstrap<ServerBootstrap, Serve ...
随机推荐
- SQL注入sqlmap联动burpsuite之burp4sqlmap++插件
目录 sqlmap和burpsuite介绍 sqlmap4burp++介绍 sqlmap4burp++的使用 小插曲:sqlmap报错文件不存在怎么办? 官方扩展CO2之SQLmapper sqlma ...
- golang之操作kafka
安装第三方包: go get github.com/IBM/sarama 生产者实例: package main import ( "fmt" "github.com/I ...
- 使用Acme.sh免费签发SSL证书
github:https://github.com/acmesh-official/acme.sh 概述一个纯粹用Shell(Unix shell)语言编写的ACME协议客户端.完整的ACME协议实施 ...
- Clickhouse之数据删除方式
什么是TTL? TTL的意思是Time To Live表示数据的存活时间.由于数据的价值会根据保存的时间成反比,出于存储成本的考虑通常只会保留近一年的数据.而在MergeTree (合并树)引擎中,可 ...
- 如何在原生鸿蒙中进行RN的断点调试
方式一 chrome devtools的方式 第一步:metro的方式加载bundle 先设置好原生这边的代码,然后记得打开RN服务器. 注意这个enableDebugger的值一定要设置为true ...
- asp.net 简单日志收集
做开发的都知道,完整的日志记录对问题的解决,回溯是多么的重要,多么的不可缺少. 那么我们怎么记录完整的日志? 今天,我们来说一说问题:从哪里开始记录呢?在哪里保存呢? IHttpModule,这个大家 ...
- log4j2 变量注入漏洞(CVE-2021-44228)
log4j2 JNDI注入漏洞(CVE-2021-44228) 概述 本文非常详细的从头到尾debug了CVE-2021-44228漏洞的利用过程,喜欢的师傅记得点个推荐~ Apache Log4j2 ...
- fastadmin-表单使用
1.日期时间 在FastAdmin中的日期时间组件采用的是Bootstrap-datetimepicker插件,官方文档:Bootstrap-datetimepicker官方教程 日期时间格式设置:设 ...
- C#调用Python脚本的方式(一),以PaddleOCR-GUI为例
前言 每种语言都有每种语言的优势,Python由于其强大的生态,很多任务通过调用包就可以实现,那么学会从C#项目中调用Python脚本完成任务就很重要.C#调用Python代码有多种方式,如果Pyth ...
- 刷到一个 MLSQL 语言
在 https://www.infoq.cn/video/2vFUBYfxFcoFWmSm5WOj 刷到一个 MLSQL 语言,主页 https://www.mlsql.tech/home ,意思是用 ...
