RANSAC---从直线拟合到特征匹配去噪

Ransac全称为Random Sample Consensus，随机一致性采样。该方法是一种十分高效的数据拟合方法。我们通过最简单的拟合直线任务来了解这种方法思路，继而扩展到特征点匹配中的误点剔除问题。

（注意，RANSAC不是直接用于特征点匹配，而是一种在初步特征匹配后消除误匹配的方法）

直线拟合过程

在平面直线拟合任务中，我们的目标是找到一条直线方程，使得数据集中大部分点都在这条直线方程附近；另一种理解，就是找到一个x，y之间的映射关系（模型），使得该映射关系能够尽量反映数据集中大部分点的x，y之间的关系。

首先，由于两个点能够确定一条直线，我们在数据集中随机选取两个点，通过这两个点确定一条直线方程。

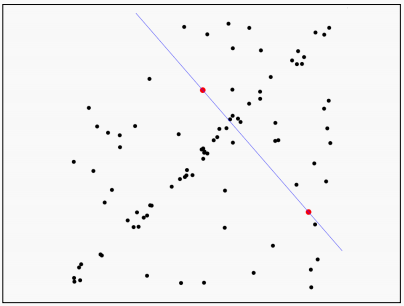
接下来，让数据集内的所有点对刚才选择的直线方程进行评估，看这条方程选的怎么样。我们计算所有点到直线的距离。

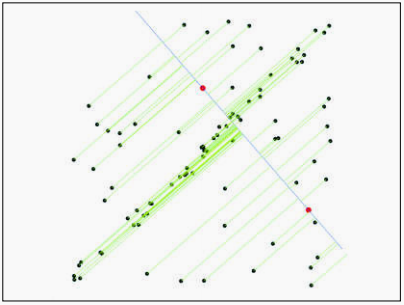
设置一个阈值范围来定义直线的”附近“，在这个范围内的点作为内点，范围外的点作为外点。计算内点数量。

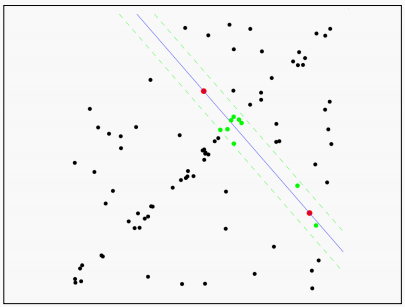
接下来重复上面的步骤，再次随机选取两个点，求解方程，所有点计算距离，得到内点数量。

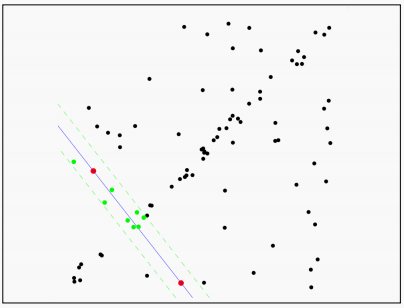
重复这一过程直到内点数量满足要求，或者达到迭代次数，此时得到的直线方程就是我们需要的直线方程。

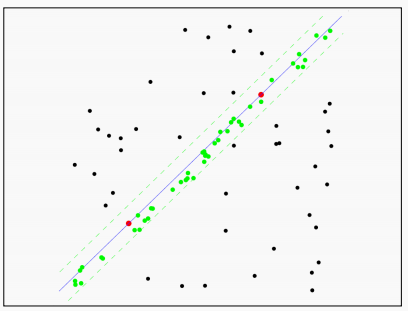
最后，为了更加精确的找到这个映射关系，我们还是需要对所有的内点进行一次最小二乘拟合。得到最终结果。

整体流程如下：

重复 N 次：

• 均匀随机抽取 2 个点
• 对这 2 个点进行直线拟合
• 在剩余的点中找出该直线的内点（即与直线距离小于 t 的点）
• 如果内点数量达到 d 个或更多，则接受该直线，并使用所有内点重新拟合

对直线拟合的RANSAC方法的思考

这个方法几乎是完全随机的、暴力的去求解这个问题。这种方法可行吗？

在计算机学科里，这种方法还真是可行。它不仅简单，还能适用于多种不同的问题。

在直线拟合任务中，数据集中每一个点（x, y），我们称其为一个sample，通过许多这样的sample，我们期望找到一个映射关系（model），能够最好的描述x, y之间的关系，使得更多的sample落在该模型的附近。事实上，任何类似这种给定samples（每个sample都是一组离散的映射），求解最优的整体映射模型的问题，都可以用RANSAC方法进行处理。

RANSAC的通用步骤

1. 随机选择一个最小subset sample集，用于描述模型
2. 拟合这个模型
3. 让其他的点对这个模型进行投票，选出距离这个模型近的点作为内点，其他作为外点
4. 重复这一过程，直到得到最优的模型

RANSAC的大体思想就是这样，我们下面讨论一些细节问题，如何选择参数？

参数选择

初始点的数量 s

通常为拟合模型所需的最少点数，比如直线拟合，确定一条直线的最小点集是2个，s就为2。

距离阈值 t

哪些点是内点，这是一个任务导向的问题。需要根据任务的数据集具体情况而定。选择 t，使内点出现的概率为 p（例如 0.95）

如果数据中的噪声分布符合均值为 0、标准差为 σ 的高斯噪声，则 t² = 3.84σ²

采样次数 N

可能我们迭代几次就找到了最优解，后续的迭代都是浪费资源；也有可能我们迭代了很多次，也找不到最优解，而这个很多次到底选多少？几百？几千？几万？这个迭代次数N如何确定。

这时我们只有采用概率的方式来确定迭代次数，也就是迭代N次，最有可能得到最优解。

设迭代N次后，至少有一次我们选择的随机样本是最优解（不含外点的模型），这个概率为p。也就是说N次迭代后我们完美找到最优解的概率为p，我们当然希望这个p值较高，我们定一个p=0.99。

那么N次迭代后我们一次都没有选择到最优解（不含外点模型）的概率是多少？显然这个说法和上面的是逻辑互斥的，这个概率为1 - p

从另一个角度来说，我们假定真实的外点率为e，在一次迭代内我们选择了s个点，这s个点我们都选择了真实内点的概率，应该是\((1-e)^s\)

相反的，这s个点我们至少选了一个外点的概率，就是\(1-(1-e)^s\)，也就是本次迭代没有得到最优解的概率。如果N次迭代每次都没有得到最优解呢，这个概率就是\((1-(1-e)^s)^N\)

上面两个粗体的描述是一致的，我们从两个角度得到了迭代N次都没有得到最优解的概率，从而将e、s、N、p这几个变量建立了关系：

\[\left(1-(1-e)^{s}\right)^{N}=1-p
\]

两边同时log一下，我们就得到了N的表达式

\[N=log (1-p) / log \left(1-(1-e)^{s}\right)
\]

在实践中，我们选择 N时，可以通过确定p = 0.99，估计一下数据集中的外点率e，通过模型类型确定s，来计算N的大小。如图中表格所示，如果外点率为40%，s为2，那么要达到0.99的最优解获得概率，迭代次数就应为7：

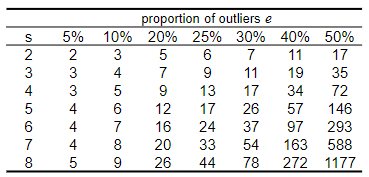
当然这是通过概率来算出来的迭代次数，只是给一个参考，实践中我们还是应当适当选取一个更大的值。

此外，内点比例 e 通常是先验未知的，所以选取最不利的情况，例如 50% 。如果发现了更多内点，则进行调整，例如若实际内点比例为 80%，那么异常值比例e=0.2 。

一致集大小 d

这个也是和数据集相关，应与预期的内点比例 1 - e 相匹配

自适应迭代次数

在RANSAC的应用中，我们通常采用一种自适应的过程去控制迭代次数。过程如下：

初始N设为无穷大，sample_count（采样计数）设为 0

当 N>sample_count 时：

• 选择一个样本并统计内点的数量
• 计算 e=1−（内点数量）/（点的总数）
• 根据e重新计算N：

\[N=log (1-p) / log \left(1-(1-e)^{s}\right)
\]

• sample_count 自增 1

这样尽管最初的迭代次数N为无穷大，但我们在循环中，通过每次迭代算出来的外点率e可以得到新的N值，N值会不断减小。如果N值小于当前sample_count了，表示理论上迭代N次就够了，但我现在已经迭代了sample_count次（>N），所以迭代就可以停止了。

RANSAC在特征匹配问题中的应用

在图像特征进行匹配之后，往往得到的许多匹配点都是误点，如图：

这些误点会影响后续的图像拼接、识别等操作，需要将它们去除掉。得到如下图：

这个过程就可以采用RANSAC的方法。

在特征点的匹配中，每一对匹配的特征，就是一个离散的映射关系，也就是一个sample。（类比于直线拟合中的（x，y））。

存在一个最优的变换模型，对两个图像中的匹配点进行映射（类比于直线拟合中的直线方程）。

在图像的特征点变换时，我们用单应性矩阵描述两个平面之间的透视关系，它把一个平面上的点通过齐次坐标映射到另一个平面上。其公式为：

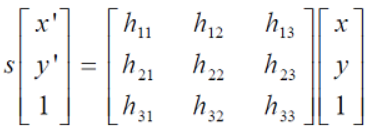
通常令h33=1来归一化矩阵。由于单应性矩阵有8个未知参数，至少需要8个线性方程求解，对应到点位置信息上，一组点对可以列出两个方程，则至少包含4组匹配点对。

适配这个最优转换模型的samples，就是内点。不适配这个模型的samples，就是外点。（注意这里的内点和外点不是图像上的特征点，而是由一对匹配好的特征点组成的sample）

随机抽样一致性算法（RANSAC）的优缺点

• 优点
  • 简单且通用
  • 适用于许多不同的问题
  • 在实际应用中通常效果良好
• 缺点
  • 有很多参数需要调整
  • 对于低内点比例的情况效果不佳（迭代次数过多，甚至可能完全失败）
  • 基于最少样本数量，并不总能获得模型的良好初始值