初涉基环外向树dp&&bzoj1040: [ZJOI2008]骑士

基环外向树dp竟然如此简单……

Description

　　Z国的骑士团是一个很有势力的组织，帮会中汇聚了来自各地的精英。他们劫富济贫，惩恶扬善，受到社会各
界的赞扬。最近发生了一件可怕的事情，邪恶的Y国发动了一场针对Z国的侵略战争。战火绵延五百里，在和平环境
中安逸了数百年的Z国又怎能抵挡的住Y国的军队。于是人们把所有的希望都寄托在了骑士团的身上，就像期待有一
个真龙天子的降生，带领正义打败邪恶。骑士团是肯定具有打败邪恶势力的能力的，但是骑士们互相之间往往有一
些矛盾。每个骑士都有且仅有一个自己最厌恶的骑士（当然不是他自己），他是绝对不会与自己最厌恶的人一同出
征的。战火绵延，人民生灵涂炭，组织起一个骑士军团加入战斗刻不容缓！国王交给了你一个艰巨的任务，从所有
的骑士中选出一个骑士军团，使得军团内没有矛盾的两人（不存在一个骑士与他最痛恨的人一同被选入骑士军团的
情况），并且，使得这支骑士军团最具有战斗力。为了描述战斗力，我们将骑士按照1至N编号，给每名骑士一个战
斗力的估计，一个军团的战斗力为所有骑士的战斗力总和。

Input

　　第一行包含一个正整数N，描述骑士团的人数。接下来N行，每行两个正整数，按顺序描述每一名骑士的战斗力
和他最痛恨的骑士。

Output

　　应包含一行，包含一个整数，表示你所选出的骑士军团的战斗力。

Sample Input

3
10 2
20 3
30 1

Sample Output

30

HINT

N ≤ 1 000 000，每名骑士的战斗力都是不大于 1 000 000的正整数。

---

题目分析

很明显这张图有两个特点：

1.由许多小连通块组成

2.每一个连通块都是基环外向树的形式

我们可以先考虑一下基环外向树的特点：

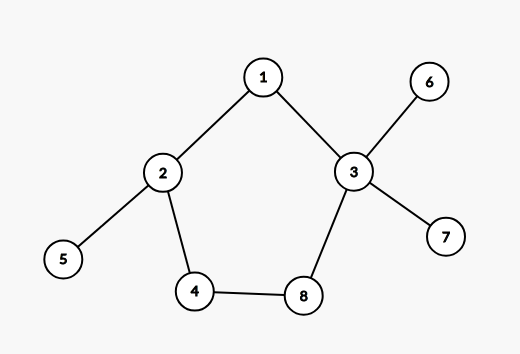
它可以看作是一颗树加一条边组成。

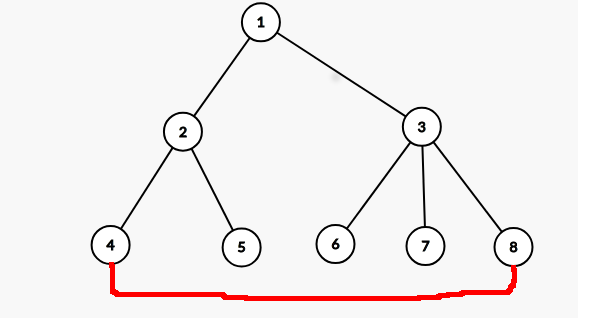
对于树的情况来说这题是很简单的，就是最大独立集的题。

然后考虑一下简单环的做法。

破环成链？

对于这种环状问题，最经典的处理方法就是破环成链：将长度为$n$的环拆成长度为$2n$的链。

但是好像维护限制有些麻烦？因为破环成链逃不开环状的模式，而这时候展开来看就会出现$f[x]=max\{f[x]+d,···\}$的奇怪形式。

拆去一条边！

环在去除一条边后就变成了一条链。而且去除任意一条边的影响都是一样的。

设去除的边为$(u,v)$，那么就代表u,v不能同时选，并且一共就三种情况：选u不选v；选v不选u；两个都不选。要是硬要在环状情况下限制住这一点，是非常麻烦的。但是我们可以用不同的状态来巧妙地回避这一点。

我们在加边时候干脆就不加这条边，这样剩下的就是一条单独的链。然后以u为树根做一次树形dp，得到的$f[u][0],f[u][1]$就分别是这条链不选$u$和选$u$的最大价值。毋庸置疑在动态规划下$f[u][1]$这个状态选没选$v$是我们无法约束的，那么就一共做两次树形dp，令$ans=max(f[u][0],f[v][0])$就好了。

于是基环外向树的情况同理，因为它去除环上任意一边后，就变成一棵树了。

 #include<bits/stdc++.h>
 const int maxn = ;

 int n,v[maxn];
 int edges[maxn<<],nxt[maxn<<],head[maxn],edgeTot;
 int fa[maxn],lDes[maxn],rDes[maxn],cnt;
 long long tmp,ans,f[maxn][];

 int read()
 {
     char ch = getchar();
     int num = ;
     bool fl = ;
     for (; !isdigit(ch); ch = getchar())
         if (ch=='-') fl = ;
     for (; isdigit(ch); ch = getchar())
         num = (num<<)+(num<<)+ch-;
     if (fl) num = -num;
     return num;
 }
 int get(int x){return x==fa[x]?x:fa[x]=get(fa[x]);}
 void addedge(int u, int v)
 {
     edges[++edgeTot] = u, nxt[edgeTot] = head[v], head[v] = edgeTot;
     edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot;
 }
 void dfs(int now, int fa)
 {
     f[now][] = v[now], f[now][] = ;
     for (int i=head[now]; i!=-; i=nxt[i])
         if (edges[i]!=fa){
             int v = edges[i];
             dfs(v, now);
             f[now][] += std::max(f[v][], f[v][]);
             f[now][] += f[v][];
         }
 }
 int main()
 {
     register int i,tt;
     memset(head, -, sizeof head);
     n = read();
     for (i=; i<=n; i++) fa[i] = i;
     for (i=; i<=n; i++)
     {
         v[i] = read(), tt = read();
         if (get(tt)!=get(i)){
             addedge(i, tt);
             fa[fa[tt]] = fa[i];
         }else lDes[++cnt] = tt, rDes[cnt] = i;
     }
     for (int i=; i<=cnt; i++)
     {
         dfs(lDes[i], );
         tmp = f[lDes[i]][];
         dfs(rDes[i], );
         tmp = std::max(tmp, f[rDes[i]][]);
         ans += tmp;
     }
     printf("%lld\n",ans);
     return ;
 }

END