tensorflow学习笔记(2)-反向传播

　　　　　　　　　　　　　　tensorflow学习笔记(2)-反向传播

　　反向传播是为了训练模型参数，在所有参数上使用梯度下降，让NN模型在的损失函数最小

　　损失函数:学过机器学习logistic回归都知道损失函数-就是预测值和真实值得差距，比如sigmod或者cross-entropy

　　均方误差:tf.reduce_mean(tf.square(y-y_))很好理解，假如在欧式空间只有两个点的的话就是两点间距离的平方，多点就是多点误差的平方和除以对比点个数

　　学习率:决定了参数每次更新的幅度

　　反向传播训练方法:为了减小loss的值为优化目标

　　

# -*- coding: utf-8 -*-
"""
Created on Sat May 26 18:42:08 2018

@author: Administrator
"""

import tensorflow as tf
import numpy as np
BATCH_SIZE=8
seed=23455

#基于seed产生随机数
rng=np.random.RandomState(seed)
#随机返回32行2列的矩阵  作为数据集输入
X=rng.rand(32,2)

#从X这个32行2列的矩阵中取出一行 判断如果和小于1  给Y赋值1 如果和不小于1 给Y赋值0
#Y作为训练集的标签
Y=[[int((x0+x1)<1)] for(x0,x1) in X]

print(X)
print(Y)
#定义输入，参数和输出
x=tf.placeholder(tf.float32,shape=(None,2))
y_=tf.placeholder(tf.float32,shape=(None,1))
#2是特征值  3是隐藏层 1是输出
w1=tf.Variable(tf.random_normal([2,3],stddev=1,seed=1))
w2=tf.Variable(tf.random_normal([3,1],stddev=1,seed=1))

a=tf.matmul(x,w1)
y=tf.matmul(a,w2)

#定义损失函数以及反向传播方法
loss=tf.reduce_mean(tf.square(y-y_))
train_step=tf.train.GradientDescentOptimizer(0.001).minimize(loss)

#会话训练
with tf.Session() as sess:
    init_op=tf.global_variables_initializer()
    sess.run(init_op)
    #输出未训练的参数值
    print(sess.run(w1))
    print(sess.run(w2))

    #训练3000次
    STEPS=10000
    for i in range(STEPS):
        start=(i*BATCH_SIZE)%32
        end=BATCH_SIZE+start
        #每次训练抽取start到end的数据
        sess.run(train_step,feed_dict={x:X[start:end],y_:Y[start:end]})
        #每500次打印一次参数
        if i%500==0:
            total_loss=sess.run(loss,feed_dict={x:X,y_:Y})
            print("在第%d次训练，损失为%g"%(i,total_loss))
    #输出训练后的参数
    print("\n")
    print(sess.run(w1))
    print(sess.run(w2))
    

这是输出的内容

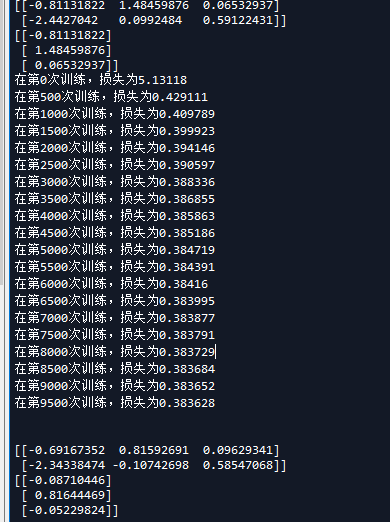
我们现在稍微改下参数比较下，首先是学习速率

当学习速率为0.1时候　　　　　　　　　　　　　　　　　　　　　　　　当学习速率为0.01

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

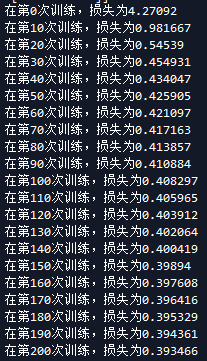
可以看出来学习速率越大梯度下降越块。

再来看看隐藏层

首先是隐藏层为4时候　　　　　　　　　　　　　　　　　　　　　　　　隐藏层为3时候

　　　　　　　　　　　　　　　　　　　　

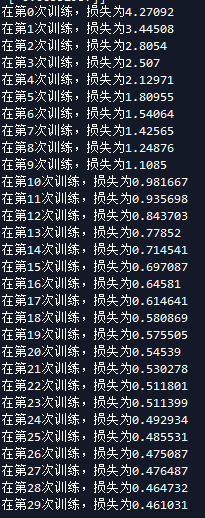
现在还不知道隐藏层怎么定义，知道以后再补上

问了群里老哥：老哥回答